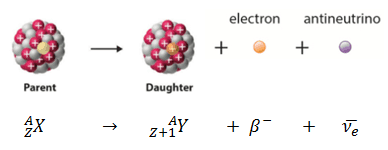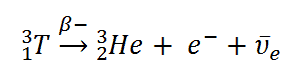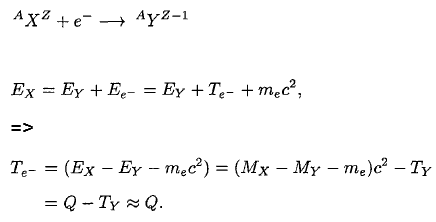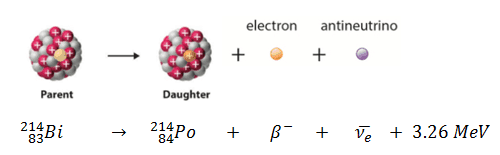Beta decay or β decay represents the disintegration of a parent nucleus to a daughter through the emission of the beta particle. This transition (β– decay) can be characterized as:
If a nucleus emits a beta particle, it loses an electron (or positron). In this case, the mass number of daughter nucleus remains the same, but daughter nucleus will form different element.
Beta particles are high-energy, high-speed electrons or positrons emitted by certain types of radioactive nuclei such as potassium-40. The beta particles have greater range of penetration than alpha particles, but still much less than gamma rays. The beta particles emitted are a form of ionizing radiation also known as beta rays. There are the following forms of beta decay:
- Negative Beta Decay – Electron Decay. In electron decay, a neutron-rich nucleus emits a high-energy electron (β– particle). The electrons are negatively charged almost massless particles Due to the law of conservation of electric charge, the nuclear charge must increase by one unit. In this case, the process can be represented by:
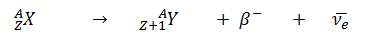
- Positive Beta Decay – Positron Decay. In positron decay, a proton-rich nucleus emits a positron (positrons are antiparticles of electrons, and have the same mass as electrons but positive electric charge), and thereby reduces the nuclear charge by one unit. In this case, the process can be represented by: An annihilation occurs, when a low-energy positron collides with a low-energy electron.
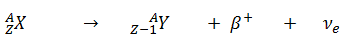
- Inverse Beta Decay – Electron Capture. Electron capture, known also as inverse beta decay is sometimes included as a type of beta decay, because the basic nuclear process, mediated by the weak interaction, is the same. In this process, a proton-rich nucleus can also reduce its nuclear charge by one unit by absorbing an atomic electron.
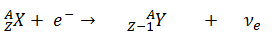
The emission of electrons was among the earliest observed decay phenomena. The inverse process, electron capture, was first observed by Luis Alvarez, in vanadium 48. He reported it in a 1937 paper in Physical Review.
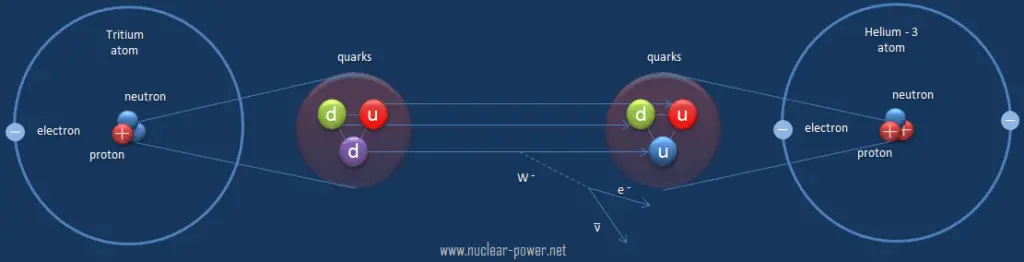
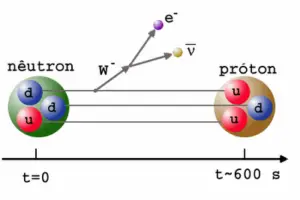
In a nuclear reactor occurs especially the β− decay, because the common feature of the fission products is an excess of neutrons (see Nuclear Stability). An unstable fission fragment with the excess of neutrons undergoes β− decay, where the neutron is converted into a proton, an electron, and an electron antineutrino. A free neutron also undergo this type of decay. A free neutron will decay with a half-life of about 611 seconds (10.3 minutes) into a proton, an electron, and an antineutrino (the antimatter counterpart of the neutrino, a particle with no charge and little or no mass).
Theory of Beta Decay – Weak Interaction
Beta decay is governed by the weak interaction. During beta decay one of two down quarks changes into an up quark by emitting a W– boson (carries away a negative charge). The W– boson then decays into a beta particle and an antineutrino. This process is equivalent to the process, in which a neutrino interacts with a neutron.
As can be seen from the figure, the weak interaction changes one flavor of quark into another. Note that, the Standard Model counts six flavours of quarks and six flavours of leptons. The weak interaction is the only process in which a quark can change to another quark, or a lepton to another lepton (flavor change). Neither the strong interaction nor electromagnetic permit flavour changing. This fact is crucial in many decays of nuclear particles. In the fusion process, which, for example, powers the Sun, two protons interact via the weak force to form a deuterium nucleus, which reacts further to generate helium. Without the weak interaction, the diproton would decay back into two hydrogen-1 unbound protons through proton emission. As a result, the sun would not burn without it since the weak interaction causes the transmutation p -> n.
In contrast to alpha decay, neither the beta particle nor its associated neutrino exist within the nucleus prior to beta decay, but are created in the decay process. By this process, unstable atoms obtain a more stable ratio of protons to neutrons. The probability of a nuclide decaying due to beta and other forms of decay is determined by its nuclear binding energy. For either electron or positron emission to be energetically possible, the energy release (see below) or Q value must be positive.
Example of Beta Decay
Energy Spectrum of Beta Decay
In both alpha and gamma decay, the resulting particle (alpha particle or photon) has a narrow energy distribution, since the particle carries the energy from the difference between the initial and final nuclear states. For example, in case of alpha decay, when a parent nucleus breaks down spontaneously to yield a daughter nucleus and an alpha particle, the sum of the mass of the two products does not quite equal the mass of the original nucleus (see Mass Defect). As a result of the law of conservation of energy, this difference appears in the form of the kinetic energy of the alpha particle. Since the same particles appear as products at every breakdown of a particular parent nucleus, the mass-difference should always be the same, and the kinetic energy of the alpha particles should also always be the same. In other words, the beam of alpha particles should be monoenergetic.
It was expected that the same considerations would hold for a parent nucleus breaking down to a daughter nucleus and a beta particle. Because only the electron and the recoiling daughter nucleus were observed beta decay, the process was initially assumed to be a two body process, very much like alpha decay. It would seem reasonable to suppose that the beta particles would form also a monoenergetic beam.
To demonstrate energetics of two-body beta decay, consider the beta decay in which an electron is emitted and the parent nucleus is at rest, conservation of energy requires:
Since the electron is much lighter particle it was expected that it will carry away most of the released energy, which would have a unique value Te-.
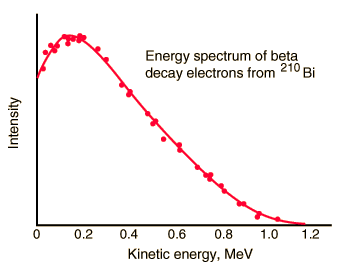
But the reality was different. The spectrum of beta particles measured by Lise Meitner and Otto Hahn in 1911 and by Jean Danysz in 1913 showed multiple lines on a diffuse background, however. Moreover virtually all of the emitted beta particles have energies below that predicted by energy conservation in two-body decays. The electrons emitted in beta decay have a continuous rather than a discrete spectrumappeared to contradict conservation of energy, under the then-current assumption that beta decay is the simple emission of an electron from a nucleus. When this was first observed, it appeared to threaten the survival of one of the most important conservation laws in physics!
To account for this energy release, Pauli proposed (in 1931) that there was emitted in the decay process another particle, later named by Fermi the neutrino. It was clear, this particle must be highly penetrating and that the conservation of electric charge requires the neutrino to be electrically neutral. This would explain why it was so hard to detect this particle. The term neutrino comes from Italian meaning “little neutral one” and neutrinos are denoted by the Greek letter ν (nu). In the process of beta decay the neutrino carries the missing energy and also in this process the law of conservation of energy remains valid.
Conservation Laws in Beta Decay
In analyzing nuclear reactions, we apply the many conservation laws. Nuclear reactions are subject to classical conservation laws for charge, momentum, angular momentum, and energy (including rest energies). Additional conservation laws, not anticipated by classical physics, are:
- Law of Conservation of Lepton Number
- Law of Conservation of Baryon Number
- Law of Conservation of Electric Charge
Certain of these laws are obeyed under all circumstances, others are not. We have accepted conservation of energy and momentum. In all the examples given we assume that the number of protons and the number of neutrons is separately conserved. We shall find circumstances and conditions in which this rule is not true. Where we are considering non-relativistic nuclear reactions, it is essentially true. However, where we are considering relativistic nuclear energies or those involving the weak interactions, we shall find that these principles must be extended.
Some conservation principles have arisen from theoretical considerations, others are just empirical relationships. Notwithstanding, any reaction not expressly forbidden by the conservation laws will generally occur, if perhaps at a slow rate. This expectation is based on quantum mechanics. Unless the barrier between the initial and final states is infinitely high, there is always a non-zero probability that a system will make the transition between them.
For purposes of analyzing non-relativistic reactions, it is sufficient to note four of the fundamental laws governing these reactions.
- Conservation of nucleons. The total number of nucleons before and after a reaction are the same.
- Conservation of charge. The sum of the charges on all the particles before and after a reaction are the same
- Conservation of momentum. The total momentum of the interacting particles before and after a reaction are the same.
- Conservation of energy. Energy, including rest mass energy, is conserved in nuclear reactions.
Reference: Lamarsh, John R. Introduction to Nuclear engineering 2nd Edition
Beta Decay – Q-value
In nuclear and particle physics the energetics of nuclear reactions is determined by the Q-value of that reaction. The Q-value of the reaction is defined as the difference between the sum of the rest masses of the initial reactants and the sum of the masses of the final products, in energy units (usually in MeV).
Consider a typical reaction, in which the projectile a and the target A gives place to two products, B and b. This can also be expressed in the notation that we used so far, a + A → B + b, or even in a more compact notation, A(a,b)B.
See also: E=mc2
The Q-value of this reaction is given by:
Q = [ma + mA – (mb + mB)]c2
When describing beta decay (reaction without projectile), the disintegrating nucleus is usually referred to as the parent nucleus and the nucleus remaining after the event as the daughter nucleus. The emission of a beta particle, either an electron, β–, or a positron, β+, changes the atomic number of the nucleus without affecting its mass number. The total rest mass of the daughter nucleus and of the nuclear radiation released in a beta disintegration, mDaughter + mRadiation, is always less than that of the parent nucleus, mparent.
The mass-energy difference,
Q = [mparent – (mDaughter + mRadiation)]c2
appears as the disintegration energy, liberated in the process. For example, the Q-value of typical beta decay is:
In the process of beta decay, either an electron or a positron is emitted. This emission is accompanied by the emission of antineutrino (β- decay) or neutrino (β+ decay), which shares energy and momentum of the decay. The beta emission has a characteristic spectrum. This characteristic spectrum is caused by the fact that either a neutrino or an antineutrino is emitted with emission of beta particle. The shape of this energy curve depends on what fraction of the reaction energy (Q value-the amount of energy released by the reaction) is carried by the massive particle. Beta particles can therefore be emitted with any kinetic energy ranging from 0 to Q. After an alpha or beta decay, the daughter nucleus is often left in an excited energy state. In order to stabilize itself, it subsequently emits high-energy photons, γ-rays.
We hope, this article, Beta Decay – Beta Radioactivity, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.