What is Mass Defect – Definition

by
The binding energy which is proportional to this mass difference is known as the mass defect. The mass defect may be calculated directly from e=mc2 equation. Periodic Table

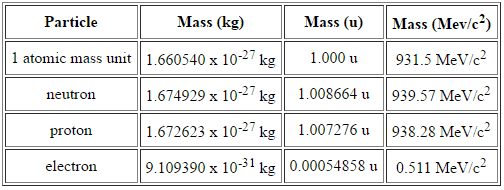
Mass Defect

In special theory of relativity certain types of matter may be created or destroyed, but in all of these processes, the mass and energy associated with such matter remains unchanged in quantity. It was found the rest mass of an atomic nucleus is measurably smaller than the sum of the rest masses of its constituent protons, neutrons and electrons. Mass was no longer considered unchangeable in the closed system. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E=mc2), this binding energy is proportional to this mass difference and it is known as the mass defect.

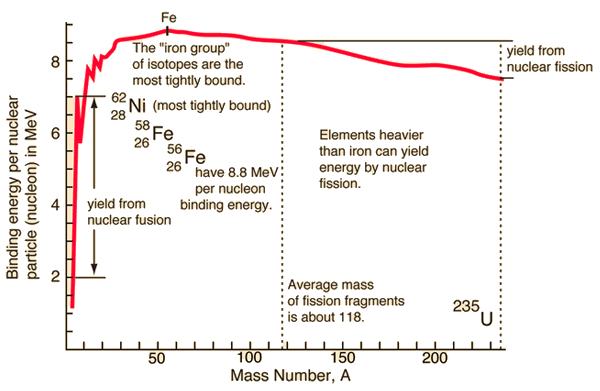
Nuclear binding energy curve.
Nuclear binding energy curve.
Source: hyperphysics.phy-astr.gsu.edu

During the nuclear splitting or nuclear fusion, some of the mass of the nucleus gets converted into huge amounts of energy and thus this mass is removed from the total mass of the original particles, and the mass is missing in the resulting nucleus. The nuclear binding energies are enormous, they are on the order of a million times greater than the electron binding energies of atoms.

 
Atomic Mass Unit
Atomic mass unit

It is defined as one twelfth of the mass of an unbound neutral atom of carbon-12 in its nuclear and electronic ground state, and has a value of 1.66054×10−27 kg.

Atomic Mass Unit
Masses of protons, neutrons and electrons in various units.

Examples of mass defect calculation

 
Example: Mass defect of a 63Cu
Calculate the mass defect of a 63Cu nucleus if the actual mass of 63Cu in its nuclear ground state is 62.91367 u.

63Cu nucleus has 29 protons and also has (63 – 29) 34 neutrons.

The mass of a proton is 1.00728 u and a neutron is 1.00867 u.

The combined mass is: 29 protons x (1.00728 u/proton) + 34 neutrons x (1.00867 u/neutron) = 63.50590 u

The mass defect is Δm = 63.50590 u – 62.91367 u =  0.59223 u

Convert the mass defect into energy (nuclear binding energy).

(0.59223 u/nucleus) x (1.6606 x 10-27 kg/u) = 9.8346 x 10-28 kg/nucleus

ΔE = Δmc2

ΔE = (9.8346 x 10-28 kg/nucleus) x (2.9979 x 108 m/s)2 = 8.8387 x 10-11 J/nucleus

The energy calculated in the previous example is the nuclear binding energy.  However, the nuclear binding energy may be expressed as kJ/mol (for better understanding).

Calculate the nuclear binding energy of 1 mole of 63Cu:

(8.8387 x 10-11 J/nucleus) x (1 kJ/1000 J) x (6.022 x 1023 nuclei/mol) = 5.3227 x 1010 kJ/mol of nuclei.

One mole of 63Cu (~63 grams) is bound by the nuclear binding energy (5.3227 x 1010 kJ/mol) which is equivalent to:

  • 14.8 million kilowatt-hours (≈ 15 GW·h)
  • 336,100 US gallons of automotive gasoline
Example: Mass defect of the reactor core
Calculate the mass defect of the 3000MWth reactor core after one year of operation.

It is known the average recoverable energy per fission is about 200 MeV, being the total energy minus the energy of the energy of antineutrinos that are radiated away.

The reaction rate per entire 3000MWth reactor core is about  9.33×1019 fissions / second.

The overall energy release in the units of joules is:

200×106 (eV) x 1.602×10-19 (J/eV) x 9.33×1019 (s-1) x 31.5×106 (seconds in year) = 9.4×1016 J/year

The mass defect is calculated as:

Δm = ΔE/c2

Δm = 9.4×1016 / (2.9979 x 108)2 = 1.046 kg

That means in a typical 3000MWth reactor core about 1 kilogram of matter is converted into pure energy.

Note that, a typical annual uranium load for a 3000MWth reactor core is about 20 tonnes of enriched uranium (i.e. about 22.7 tonnes of UO2). Entire reactor core may contain about 80 tonnes of enriched uranium.

Mass defect directly from E=mc2

The mass defect can be calculated directly from the Einstein relationship (E = mc2) as:

Δm = ΔE/c2

Δm = 3000×106 (W = J/s) x 31.5×106 (seconds in year) / (2.9979 x 108)2 = 1.051 kg

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Laws of Conservation

We hope, this article, Mass Defect, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.

Related Posts