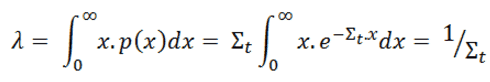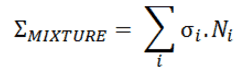Macroscopic Cross-section
The difference between the microscopic cross-section and macroscopic cross-section is very important and is restated for clarity. The microscopic cross section represents the effective target area of a single target nucleus for an incident particle. The units are given in barns or cm2.
While the macroscopic cross-section represents the effective target area of all of the nuclei contained in the volume of the material. The units are given in cm-1.
A macroscopic cross-section is derived from microscopic cross-section and the atomic number density:
Σ=σ.N
Here σ, which has units of m2, is the microscopic cross-section. Since the units of N (nuclei density) are nuclei/m3, the macroscopic cross-section Σ have units of m-1, thus in fact is an incorrect name, because it is not a correct unit of cross-sections. In terms of Σt (the total cross-section), the equation for the intensity of a neutron beam can be written as
-dI = N.σ.Σt.dx
Dividing this expression by I(x) gives
-dΙ(x)/I(x) = Σt.dx
Since dI(x) is the number of neutrons that collide in dx, the quantity –dΙ(x)/I(x) represents the probability that a neutron that has survived without colliding until x, will collide in the next layer dx. It follows that the probability P(x) that a neutron will travel a distance x without any interaction in the material, which is characterized by Σt, is:
P(x) = e-Σt.x
From this equation, we can derive the probability that a neutron will make its first collision in dx. It will be the quantity P(x)dx. If the probability of the first collision in dx is independent of its past history, the required result will be equal to the probability that a neutron survives up to layer x without any interaction (~Σtdx) times the probability that the neutron will interact in the additional layer dx (i.e. ~e-Σt.x).
P(x)dx = Σtdx . e-Σt.x = Σt e-Σt.x dx
Mean Free Path
From the equation for the probability of the first collision in dx we can calculate the mean free path that is traveled by a neutron between two collisions. This quantity is usually designated by the symbol λ and it is equal to the average value of x, the distance traveled by a neutron without any interaction, over the interaction probability distribution.
whereby one can distinguish λs, λa, λf, etc. This quantity is also known as the relaxation length, because it is the distance in which the intensity of the neutrons that have not caused a reaction has decreased with a factor e.
For materials with high absorption cross-section, the mean free path is very short and neutron absorption occurs mostly on the surface of the material. This surface absorption is called self-shielding because the outer layers of atoms shield the inner layers.
Macroscopic Cross-section of Mixtures and Molecules
Most materials are composed of several chemical elements and compounds. Most of chemical elements contains several isotopes of these elements (e.g. gadolinium with its six stable isotopes). For this reason most materials involve many cross-sections. Therefore, to include all the isotopes within a given material, it is necessary to determine the macroscopic cross section for each isotope and then sum all the individual macroscopic cross-sections.
In this section both factors (different atomic densities and different cross-sections) will be considered in the calculation of the macroscopic cross-section of mixtures.
First, consider the Avogadro’s number N0 = 6.022 x 1023, is the number of particles (molecules, atoms) that is contained in the amount of substance given by one mole. Thus if M is the molecular weight, the ratio N0/M equals to the number of molecules in 1g of the mixture. The number of molecules per cm3 in the material of density ρ and the macroscopic cross-section for mixtures are given by following equations:
Ni = ρi.N0 / Mi
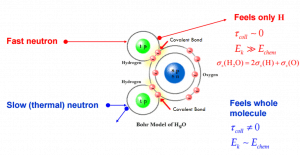
Note that, in some cases, the cross-section of the molecule is not equal to the sum of cross-sections of its individual nuclei. For example the cross-section of neutron elastic scattering of water exhibits anomalies for thermal neutrons. It occurs, because the kinetic energy of an incident neutron is of the order or less than the chemical binding energy and therefore the scattering of slow neutrons by water (H2O) is greater than by free nuclei (2H + O).
We hope, this article, Macroscopic Cross-section, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.