Nuclear Shell Model
 In nuclear physics, the nuclear shell model is a theoretical model to describe the atomic nucleus. The nuclear shell model was proposed by Dmitry Ivanenko in 1932 and further developed independently by several physicists such as Maria Goeppert-Mayer, Eugene Paul Wigner and J. Hans D. Jensen in 1949. It must be noted this model is based on the Pauli exclusion principle to describe the structure of the nucleus in terms of energy levels.
In nuclear physics, the nuclear shell model is a theoretical model to describe the atomic nucleus. The nuclear shell model was proposed by Dmitry Ivanenko in 1932 and further developed independently by several physicists such as Maria Goeppert-Mayer, Eugene Paul Wigner and J. Hans D. Jensen in 1949. It must be noted this model is based on the Pauli exclusion principle to describe the structure of the nucleus in terms of energy levels.
The nuclear shell model is partly analogous to the atomic shell model which describes the arrangement of electrons in an atom, in that a filled shell results in greater stability. Nucleons are added to shells which increase with energy that orbit around a central potential. In the atomic shell model the central potential around which the electrons orbit is generated by the nucleus. Nucleons are added to shells which increase with energy that orbit around a central potential.
In comparison to atomic shell model, the atomic nucleus governed by two different forces. The residual strong force, also known as the nuclear force, acts to hold neutrons and protons together in nuclei. In nuclei, this force acts against the enormous repulsive electromagnetic force of the protons. The term residual is associated with the fact, it is the residuum of the fundamental strong interaction between the quarks that make up the protons and neutrons. The strong interaction is very complicated interaction, because it significantly varies with distance. At distances comparable to the diameter of a proton, the strong force is approximately 100 times as strong as electromagnetic force. At smaller distances, however, the strong force between quarks becomes weaker, and the quarks begin to behave like independent particles. In particle physics, this effect is known as asymptotic freedom.
With the enormous strong force acting between individual nucleons and with so many nucleons to collide with, how can nucleons orbit a central potential without interacting? This problem is explained by the Pauli exclusion principle, which states that two fermions cannot occupy the same quantum state. In other words, the interaction will not occur, if the higher energy shells are fully occupied and the energy imparted to the nucleon during the collision is insufficient to promote the nucleon to an unfilled orbit. As a result, the nucleons orbit independent of one another.
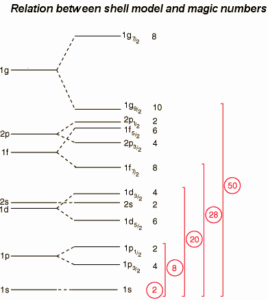
The nuclear shell model was able to describe many phenomena like the magic numbers, the ground state spin and parity etc..
Magic Numbers of Protons and Neutrons
A magic number is a number of nucleons in a nucleus, which corresponds to complete shells within the atomic nucleus. Atomic nuclei consisting of such a magic number of nucleons have a higher average binding energy per nucleon than one would expect based upon predictions such as the mass formula of von Weizsaecker (also called the semi-empirical mass formula – SEMF) and are hence more stable against nuclear decay. Magic numbers are predicted by the nuclear shell model and are proved by observations that have shown that there are sudden discontinuities in the proton and neutron separation energies at specific values of Z and N. These correspond to the closing of shells (or sub-shells). Nuclei with closed shells are more tightly bound than the next higher number. The closing of shells occurs at Z or N = 2, 8, 20, 28, (40), 50, 82, 126. It is found that nuclei with even numbers of protons and neutrons are more stable than those with odd numbers. Nuclei which have both neutron number and proton number equal to one of the magic numbers can be called “doubly magic“, and are found to be particularly stable.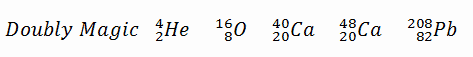 There are further special propertis of nuclei, which have a magic number of nucleons:
There are further special propertis of nuclei, which have a magic number of nucleons:
- Higher abundance in nature. For example, helium-4 is among the most abundant (and stable) nuclei in the universe.
- The stable elements at the end of the decay series all have a “magic number” of neutrons or protons. The nuclei He-4, O-16, and Pb-208 (82 protons and 126 neutrons) that contain magic numbers of both neutrons and protons are particularly stable. The relative stability of these nuclei is reminiscent of that of inert gas atoms (closed electron shells).
- Nuclei with N = magic number have much lower neutron absorption cross-sections than surrounding isotopes.
- These nuclei appear to be perfectly spherical in shape; they have zero quadrupole electric moments.
- Magic number nuclei have higher first excitation energy.
Neutron Star as “Giant Nucleus”
A neutron star is the collapsed core of a large star (usually of a red giant). Neutron stars are the smallest and densest stars known to exist and they are rotating extremely rapidly. A neutron star is basically a giant atomic nucleus about 11 km in diameter made especially of neutrons. It is believed that under the immense pressures of a collapsing massive stars going supernova it is possible for the electrons and protons to combine to form neutrons via electron capture, releasing a huge amount of neutrinos. Since they have some similar properties as atomic nuclei, neutron stars are sometimes described as giant nuclei. But be careful, neutron stars and atomic nuclei are held together by different forces. A nucleus is held together by the strong force, while a neutron star is held together by gravitational force.
On the other hand, neutron stars are partially supported against further collapse by neutron degeneracy (via degeneracy pressure), a phenomenon described by the Pauli exclusion principle. In general, in a highly dense state of matter, where gravitational pressure is extreme, quantum mechanical effects are significant. Degenerate matter is usually modelled as an ideal Fermi gas, in which the Pauli exclusion principle prevents identical fermions from occupying the same quantum state. Similarly, white dwarfs are supported against collapse by electron degeneracy pressure, which is analogous to neutron degeneracy.
We hope, this article, Nuclear Shell Model – Shell Model of Nucleus, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.