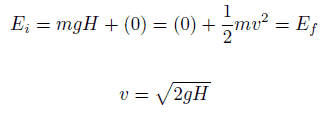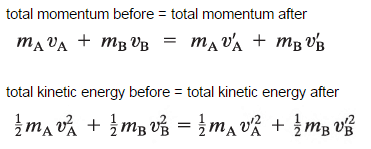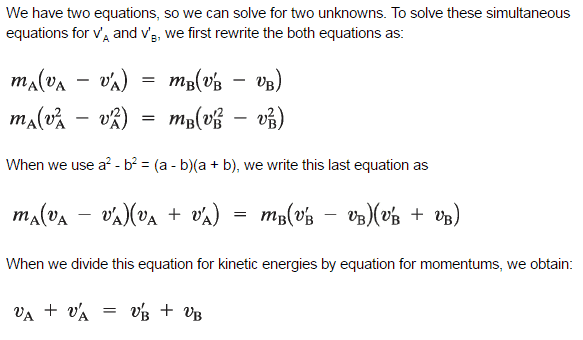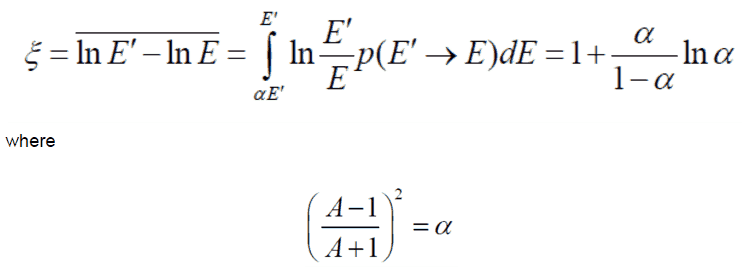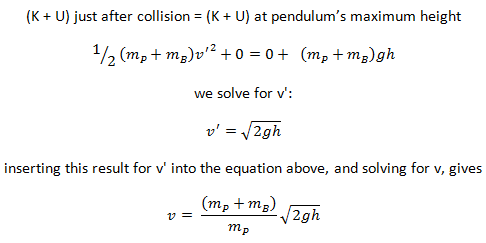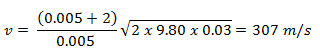Conservation of Momentum and Energy
The law of conservation of energy is one of the basic laws of physics along with the conservation of mass and the conservation of momentum. The law of conservation of energy states that energy can change from one form into another, but it cannot be created or destroyed. Or the general definition is:
The total energy of an isolated system remains constant over time.

Energy can be defined as the capacity for doing work. It may exist in a variety of forms and may be transformed from one type of energy to another in hundreds of ways.
For example, burning gasoline to power cars is an energy conversion process we rely on. The chemical energy in gasoline is converted to thermal energy, which is then converted to mechanical energy that makes the car move. The mechanical energy has been converted to kinetic energy. When we use the brakes to stop a car, that kinetic energy is converted by friction back to heat, or thermal energy.
A consequence of the law of conservation of energy is that a perpetual motion machine of the first kind, which produces work without the input of energy, cannot exist.
Conservation of Mechanical Energy
First the principle of the Conservation of Mechanical Energy was stated:
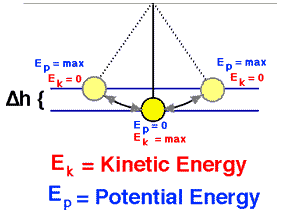
The total mechanical energy (defined as the sum of its potential and kinetic energies) of a particle being acted on by only conservative forces is constant.
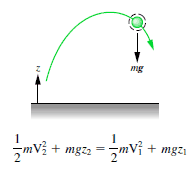 An isolated system is one in which no external force causes energy changes. If only conservative forces act on an object and U is the potential energy function for the total conservative force, then
An isolated system is one in which no external force causes energy changes. If only conservative forces act on an object and U is the potential energy function for the total conservative force, then
Emech = U + K
The potential energy, U, depends on the position of an object subjected to a conservative force.
It is defined as the object’s ability to do work and is increased as the object is moved in the opposite direction of the direction of the force.
The potential energy associated with a system consisting of Earth and a nearby particle is gravitational potential energy.
The kinetic energy, K, depends on the speed of an object and is the ability of a moving object to do work on other objects when it collides with them.
K = ½ mv2
The above mentioned definition (Emech = U + K) assumes that the system is free of friction and other non-conservative forces. The difference between a conservative and a non-conservative force is that when a conservative force moves an object from one point to another, the work done by the conservative force is independent of the path.
In any real situation, frictional forces and other non-conservative forces are present, but in many cases their effects on the system are so small that the principle of conservation of mechanical energy can be used as a fair approximation. For example the frictional force is a non-conservative force, because it acts to reduce the mechanical energy in a system.
Note that non-conservative forces do not always reduce the mechanical energy. A non-conservative force changes the mechanical energy, there are forces that increase the total mechanical energy, like the force provided by a motor or engine, is also a non-conservative force.
Conservation of Momentum and Energy in Collisions
The use of the conservation laws for momentum and energy is very important also in particle collisions. This is a very powerful rule because it can allow us to determine the results of a collision without knowing the details of the collision. The law of conservation of momentum states that in the collision of two objects such as billiard balls, the total momentum is conserved. The assumption of conservation of momentum as well as the conservation of kinetic energy makes possible the calculation of the final velocities in two-body collisions. At this point we have to distinguish between two types of collisions:
- Elastic collisions
- Inelastic collisions
Elastic Collisions
A perfectly elastic collision is defined as one in which there is no net conversion of kinetic energy into other forms (such as heat or noise). For the brief moment during which the two objects are in contact, some (or all) of the energy is stored momentarily in the form of elastic potential energy. But if we compare the total kinetic energy just before the collision with the total kinetic energy just after the collision, and they are found to be the same, then we say that the total kinetic energy is conserved.
- Some large-scale interactions like the slingshot type gravitational interactions (also known as a planetary swing-by or a gravity-assist manoeuvre) between satellites and planets are perfectly elastic.
- Collisions between very hard spheres may be nearly elastic, so it is useful to calculate the limiting case of an elastic collision.
- Collisions in ideal gases approach perfectly elastic collisions, as do scattering interactions of sub-atomic particles which are deflected by the electromagnetic force.
- Rutherford scattering is the elastic scattering of charged particles also by the electromagnetic force.
- A neutron-nucleus scattering reaction may be also elastic, but in this case the neutron is deflected by the strong nuclear force.
Inelastic Collisions
An inelastic collision is one in which part of the kinetic energy is changed to some other form of energy in the collision. Any macroscopic collision between objects will convert some of the kinetic energy into internal energy and other forms of energy, so no large scale impacts are perfectly elastic. For example, in collisions of common bodies, such as two cars, some energy is always transferred from kinetic energy to other forms of energy, such as thermal energy or energy of sound. The inelastic collision of two bodies always involves a loss in the kinetic energy of the system. The greatest loss occurs if the bodies stick together, in which case the collision is called a completely inelastic collision. Thus, the kinetic energy of the system is not conserved, while the total energy is conserved as required by the general principle of conservation of energy. Momentum is conserved in inelastic collisions, but one cannot track the kinetic energy through the collision since some of it is converted to other forms of energy.
In nuclear physics, an inelastic collision is one in which the incoming particle causes the nucleus it strikes to become excited or to break up. Deep inelastic scattering is a method of probing the structure of subatomic particles in much the same way as Rutherford probed the inside of the atom (see Rutherford scattering).
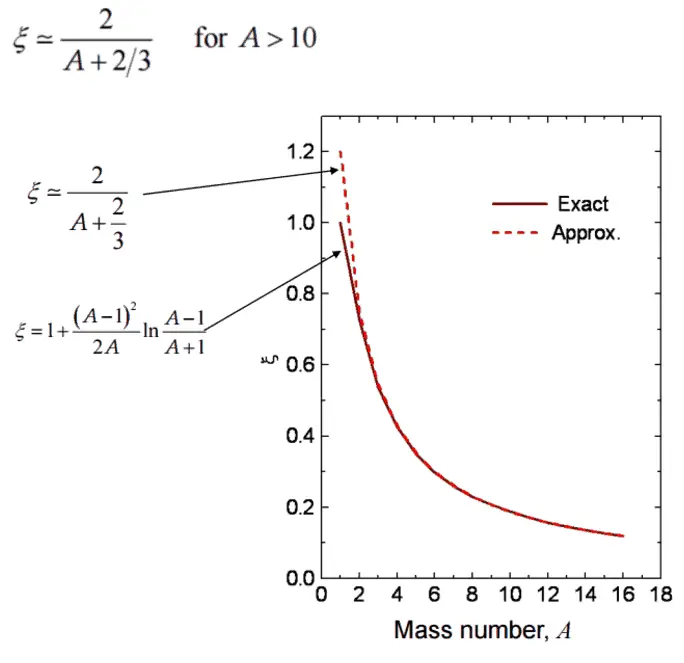
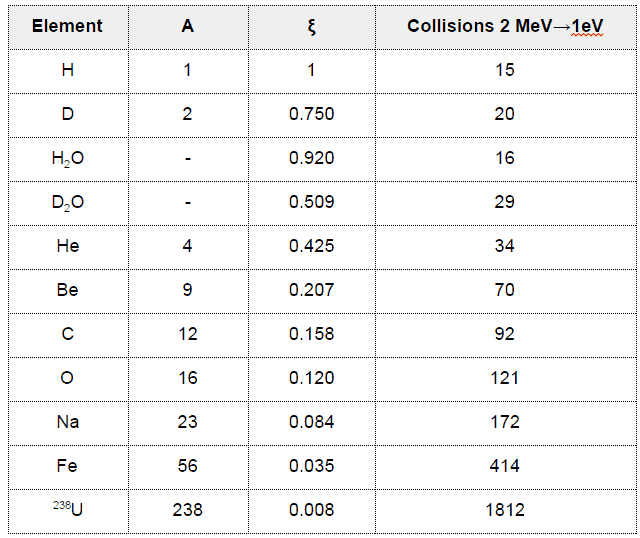
In nuclear reactors, inelastic collisions are of importance in neutron moderation process. An inelastic scattering plays an important role in slowing down neutrons especially at high energies and by heavy nuclei. Inelastic scattering occurs above a threshold energy. This threshold energy is higher than the energy the first excited state of target nucleus (due to the laws of conservation) and it is given by following formula:
Et = ((A+1)/A)* ε1
where Et is known as the inelastic threshold energy and ε1 is the energy of the first excited state. Therefore especially scattering data of 238U, which is a major component of nuclear fuel in commercial power reactors, are one of the most important data in the neutron transport calculations in the reactor core.
We hope, this article, Conservation of Momentum and Energy, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.