Specific Internal Energy
The specific internal energy (u) of a substance is its internal energy per unit mass. It is an intensive property. It equals to the total internal energy (U) divided by the total mass (m).
u = U/m
where:
u = specific internal energy (J/kg)
U = internal energy (J)
m = mass (kg)
Internal Energy – Thermal Energy
Potential energy and kinetic energy, that was discussed in previous chapters, are macroscopic forms of energy. They are dependent on macroscopic variables such as the position and the velocity of objects.
In thermodynamics, internal energy (also called the thermal energy) is defined as the energy associated with microscopic forms of energy. It is an extensive quantity, it depends on the size of the system, or on the amount of substance it contains. The SI unit of internal energy is the joule (J). It is the energy contained within the system, excluding the kinetic energy of motion of the system as a whole and the potential energy of the system. Microscopic forms of energy include those due to the rotation, vibration, translation, and interactions among the molecules of a substance. None of these forms of energy can be measured or evaluated directly, but techniques have been developed to evaluate the change in the total sum of all these microscopic forms of energy.
In addition, energy is can be stored in the chemical bonds between the atoms that make up the molecules. This energy storage on the atomic level includes energy associated with electron orbital states, nuclear spin, and binding forces in the nucleus.
Internal energy is represented by the symbol U, and the change in internal energy in a process is U2 – U1.
Microscopic Energy
Internal energy involves energy on the microscopic scale. It may be divided into microscopic potential energy, Upot, and microscopic kinetic energy, Ukin, components:
U = Upot + Ukin
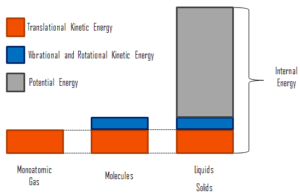 where the microscopic kinetic energy, Ukin, involves the motions of all the system’s particles with respect to the center-of-mass frame. For an ideal monatomic gas, this is just the translational kinetic energy of the linear motion of the atoms. Monoatomic particles do not rotate or vibrate. The behavior of the system is well described by kinetic theory of gases. Kinetic theory is based on the fact that during an elastic collision between a molecule with high kinetic energy and one with low kinetic energy, part of energy will transfer to the molecule of lower kinetic energy. However, for polyatomic gases there is rotational and vibrational kinetic energy as well.
where the microscopic kinetic energy, Ukin, involves the motions of all the system’s particles with respect to the center-of-mass frame. For an ideal monatomic gas, this is just the translational kinetic energy of the linear motion of the atoms. Monoatomic particles do not rotate or vibrate. The behavior of the system is well described by kinetic theory of gases. Kinetic theory is based on the fact that during an elastic collision between a molecule with high kinetic energy and one with low kinetic energy, part of energy will transfer to the molecule of lower kinetic energy. However, for polyatomic gases there is rotational and vibrational kinetic energy as well.
The microscopic potential energy, Upot, involves the chemical bonds between the atoms that make up the molecules, binding forces in the nucleus and also the physical force fields within the system (e.g. electric or magnetic fields).
In liquids and solids there is significant component of potential energy associated with the intermolecular attractive forces.
We hope, this article, Specific Internal Energy, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.