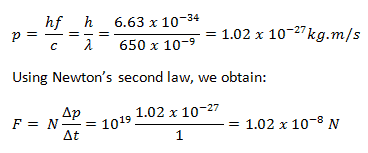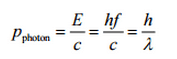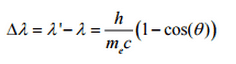What is Momentum of Photon – Definition

by
Momentum of Photon. Although a photon (quantum of light) is massless, it has momentum, which is related to its energy E, frequency f, and wavelength

Momentum of Photon

A photon, the quantum of electromagnetic radiation,  is an elementary particle, which is the force carrier of the electromagnetic force. The modern photon concept was developed (1905) by Albert Einstein to explain of the photoelectric effect, in which he proposed the existence of discrete energy packets during the transmission of light.

In 1916, Einstein extended his concept of light quanta (photons) by proposing that a quantum of light has linear momentum. Although a photon is massless, it has momentum, which is related to its energy E, frequency f, and wavelength by:

momentum-photon-equation

Thus, when a photon interacts with another object, energy and momentum are transferred, as if there were a collision between the photon and matter in the classical sense.

 
Example: Momentum and Force of a Photon
Suppose the 1019 photons (let λ = 650 nm) emitted per second from the 100 W lightbulb.  Suppose all photons are focused onto a piece of black paper and absorbed. Assume that the momentum of a photon changes from p = h/λ to zero.

Calculate the momentum of one photon and calculate the force all these photons could exert on the paper.

Solution:

We use the formula of momentum of a single photon:

momentum-photon-example

Momentum of a Photon – Compton Scattering

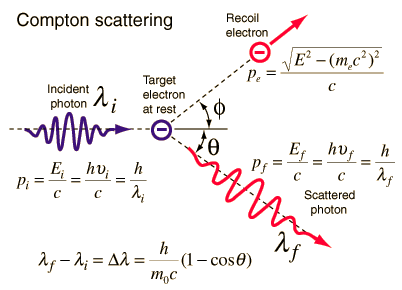
Compton Scattering
In Compton scattering, the incident gamma-ray photon is deflected through an angle Θ with respect to its original direction. This deflection results in a decrease in energy (decrease in photon’s frequency) of the photon and is called the Compton effect.
Source: hyperphysics.phy-astr.gsu.edu

The Compton formula was published in 1923 in the Physical Review. Compton explained that the X-ray shift is caused by particle-like momentum of photons. Compton scattering formula is the mathematical relationship between the shift in wavelength and the scattering angle of the X-rays. In the case of Compton scattering the photon of frequency f collides with an electron at rest. Upon collision, the photon bounces off electron, giving up some of its initial energy (given by Planck’s formula E=hf), While the electron gains momentum (mass x velocity), the photon cannot lower its velocity. As a result of momentum conservation law, the photon must lower its momentum given by:

As a result of momentum conservetion law, the photon must lower its momentum given by this formula.

So the decrease in photon’s momentum must be translated into decrease in frequency (increase in wavelength Δλ = λ’ – λ). The shift of the wavelength increased with scattering angle according to the Compton formula:

The shift of the wavelength increased with scattering angle according to the Compton formula

where λ is the initial wavelength of photon λ’ is the wavelength after scattering, h is the Planck constant = 6.626 x 10-34 J.s, me is the electron rest mass (0.511 MeV)c is the speed of light Θ is the scattering angle. The minimum change in wavelength (λ′ − λ) for the photon occurs when Θ = 0° (cos(Θ)=1) and is at least zero. The maximum change in wavelength (λ′ − λ) for the photon occurs when Θ = 180° (cos(Θ)=-1). In this case the photon transfers to the electron as much momentum as possible. The maximum change in wavelength can be derived from Compton formula:

The maximum change in wavelength can be derived from Compton formula. Compton length

The quantity h/mec is known as the Compton wavelength of the electron and is equal to 2.43×10−12 m.

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Photon

We hope, this article, Momentum of Photon, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.

Related Posts