What is What is Angular Momentum – Definition – Definition

by
Angular momentum (rarely, moment of momentum or rotational momentum), L, is the rotational analog of linear momentum. What is Angular Momentum

Whar is Angular Momentum

conservation of angular momentumIn physics, the linear momentum, p = mv, has a rotational analog. It is called angular momentum  (rarely, moment of momentum or rotational momentum), L, and for an object rotating about a fixed axis with angular velocity ω, it is defined as:

L = Iω

It is an important quantity in physics because it is a conserved quantity:

The angular momentum of an isolated system remains constant in both magnitude and direction.

When there is zero net torque acting on an object, and the object is rotating about a fixed axis or about an axis through its center of mass whose direction doesn’t change, we can write:

I1ω1 = I2ω2 = constant

Like conservation of energy and of linear momentum, this principle is a universal conservation law, valid at all scales from atomic and nuclear systems to the motions of galaxies. The angular momentum is a vector quantity and therefore it can be generalized as:

The vector sum of the angular momenta of the parts of an isolated system is constant.

This puts a strong constraint on the types of rotational motions which can occur in an isolated system. If one part of the system is given an angular momentum in a given direction, then some other part or parts of the system must simultaneously be given exactly the same angular momentum in the opposite direction.

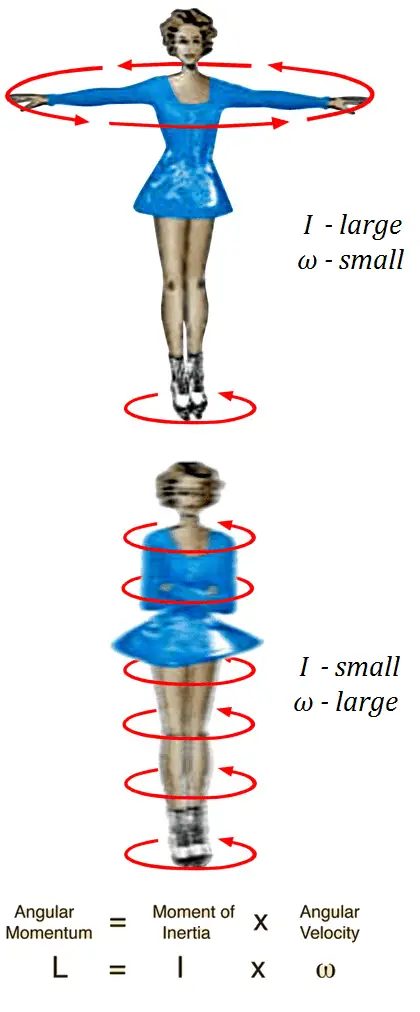
The law of conservation of angular momentum explains the angular acceleration of an ice skater as she brings her arms and legs closer to the vertical axis of rotation. By bringing part of the mass of her body closer to the axis she decreases her body’s moment of inertia. Because angular momentum is the product of moment of inertia (I) and angular velocity (ω), and the angular momentum remains constant according to this law, the angular velocity of the skater must increase.

I1ω1 = I2ω2

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Angular Momentum

We hope, this article, What is Angular Momentum – Definition, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.

Related Posts