Hydrogen
1.0079 amu
Helium
4.0026 amu
Lithium
6.941 amu
Beryllium
9.0122 amu
Boron
10.811 amu
Carbon
12.0107 amu
Nitrogen
14.0067 amu
Oxygen
15.9994 amu
Fluorine
18.9984 amu
Neon
20.1797 amu
Sodium
22.9897 amu
Magnesium
24.305 amu
Aluminium
26.9815 amu
Silicon
28.0855 amu
Phosphorus
30.9738 amu
Sulfur
32.065 amu
Chlorine
35.453 amu
Argon
39.948 amu
Potassium
39.0983 amu
Calcium
40.078 amu
Scandium
44.9559 amu
Titanium
47.867 amu
Vanadium
50.9415 amu
Chromium
51.9961 amu
Manganese
54.9381 amu
Iron
55.845 amu
Cobalt
58.9332 amu
Nickel
58.6934 amu
Copper
63.546 amu
Zinc
65.409 amu
Gallium
69.723 amu
Germanium
72.64 amu
Arsenic
74.9216 amu
Selenium
78.96 amu
Bromine
79.904 amu
Krypton
83.798 amu
Rubidium
85.4678 amu
Strontium
87.62 amu
Yttrium
88.9059 amu
Zirconium
91.224 amu
Niobium
92.9064 amu
Molybdenum
95.94 amu
Technetium
98 amu
Ruthenium
101.07 amu
Rhodium
102.9055 amu
Palladium
106.42 amu
Silver
107.8682 amu
Cadmium
112.411 amu
Indium
114.818 amu
Tin
118.71 amu
Antimony
121.76 amu
Tellurium
127.6 amu
Iodine
126.9045 amu
Xenon
131.293 amu
Caesium
132.9055 amu
Lanthanoids
Hafnium
178.49 amu
Tantalum
180.9479 amu
Tungsten
183.84 amu
Rhenium
186.207 amu
Osmium
190.23 amu
Iridium
192.217 amu
Platinum
195.079 amu
Gold
196.9665 amu
Mercury
200.59 amu
Thallium
204.3833 amu
Lead
207.2 amu
Bismuth
208.9804 amu
Polonium
209 amu
Astatine
210 amu
Radon
222 amu
Francium
223 amu
Radium
226 amu
Actinoids
Rutherfordium
261 amu
Dubnium
262 amu
Seaborgium
266 amu
Bohrium
264 amu
Hassium
277 amu
Meitnerium
268 amu
Darmstadtium
281 amu
Roentgenium
272 amu
Copernicium
285 amu
Nihonium
286 amu
Flerovium
289 amu
Moscovium
290 amu
Livermorium
292 amu
Tennessine
294 amu
Oganesson
294 amu
Lanthanum
138.9055 amu
Cerium
140.116 amu
Praseodymium
140.9077 amu
Neodymium
144.24 amu
Promethium
145 amu
Samarium
150.36 amu
Europium
151.964 amu
Gadolinium
157.25 amu
Terbium
158.9253 amu
Dysprosium
162.5 amu
Holmium
164.9303 amu
Erbium
167.259 amu
Thulium
168.9342 amu
Ytterbium
173.04 amu
Lutetium
174.967 amu
Actinium
227 amu
Thorium
232.0381 amu
Protactinium
231.0359 amu
Uranium
238.0289 amu
Neptunium
237 amu
Plutonium
244 amu
Americium
243 amu
Curium
247 amu
Berkelium
247 amu
Californium
251 amu
Einsteinium
252 amu
Fermium
257 amu
Mendelevium
258 amu
Nobelium
259 amu
Lawrencium
262 amu
Atomic Mass of Rhodium
Atomic mass of Rhodium is 102.9055 u.
The atomic mass is the mass of an atom. The atomic mass or relative isotopic mass refers to the mass of a single particle, and therefore is tied to a certain specific isotope of an element. The atomic mass is carried by the atomic nucleus, which occupies only about 10-12 of the total volume of the atom or less, but it contains all the positive charge and at least 99.95% of the total mass of the atom. Note that, each element may contain more isotopes, therefore this resulting atomic mass is calculated from naturally-occuring isotopes and their abundance.
The size and mass of atoms are so small that the use of normal measuring units, while possible, is often inconvenient. Units of measure have been defined for mass and energy on the atomic scale to make measurements more convenient to express. The unit of measure for mass is the atomic mass unit (amu). One atomic mass unit is equal to 1.66 x 10-24 grams. One unified atomic mass unit is approximately the mass of one nucleon (either a single proton or neutron) and is numerically equivalent to 1 g/mol.
For 12C the atomic mass is exactly 12u, since the atomic mass unit is defined from it. For other isotopes, the isotopic mass usually differs and is usually within 0.1 u of the mass number. For example, 63Cu (29 protons and 34 neutrons) has a mass number of 63 and an isotopic mass in its nuclear ground state is 62.91367 u.
There are two reasons for the difference between mass number and isotopic mass, known as the mass defect:
- The neutron is slightly heavier than the proton. This increases the mass of nuclei with more neutrons than protons relative to the atomic mass unit scale based on 12C with equal numbers of protons and neutrons.
- The nuclear binding energy varies between nuclei. A nucleus with greater binding energy has a lower total energy, and therefore a lower mass according to Einstein’s mass-energy equivalence relation E = mc2. For 63Cu the atomic mass is less than 63 so this must be the dominant factor.
Note that, it was found the rest mass of an atomic nucleus is measurably smaller than the sum of the rest masses of its constituent protons, neutrons and electrons. Mass was no longer considered unchangeable in the closed system. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E=mc2), this binding energy is proportional to this mass difference and it is known as the mass defect.
See also: Atomic Mass Number – Does it conserve in a nuclear reaction?
Mass Number of Rhodium
Mass numbers of typical isotopes of Rhodium are 103.
The total number of neutrons in the nucleus of an atom is called the neutron number of the atom and is given the symbol N. Neutron number plus atomic number equals atomic mass number: N+Z=A. The difference between the neutron number and the atomic number is known as the neutron excess: D = N – Z = A – 2Z.
Neutron number is rarely written explicitly in nuclide symbol notation, but appears as a subscript to the right of the element symbol. Nuclides that have the same neutron number but a different proton number are called isotones. The various species of atoms whose nuclei contain particular numbers of protons and neutrons are called nuclides. Each nuclide is denoted by chemical symbol of the element (this specifies Z) with tha atomic mass number as supescript. Therefore, we cannot determine the neutron number of uranium, for example. We can determine the neutron number of certain isotope. For example, the neutron number of uranium-238 is 238-92=146.
Density of Rhodium
Density of Rhodium is 12.45g/cm3.
Typical densities of various substances are at atmospheric pressure.
Density is defined as the mass per unit volume. It is an intensive property, which is mathematically defined as mass divided by volume:
ρ = m/V
In words, the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance. The standard SI unit is kilograms per cubic meter (kg/m3). The Standard English unit is pounds mass per cubic foot (lbm/ft3).
Density – Atomic Mass and Atomic Number Density
Since the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance, it is obvious, the density of a substance strongly depends on its atomic mass and also on the atomic number density (N; atoms/cm3),
- Atomic Weight. The atomic mass is carried by the atomic nucleus, which occupies only about 10-12 of the total volume of the atom or less, but it contains all the positive charge and at least 99.95% of the total mass of the atom. Therefore it is determined by the mass number (number of protons and neutrons).
- Atomic Number Density. The atomic number density (N; atoms/cm3), which is associated with atomic radii, is the number of atoms of a given type per unit volume (V; cm3) of the material. The atomic number density (N; atoms/cm3) of a pure material having atomic or molecular weight (M; grams/mol) and the material density (⍴; gram/cm3) is easily computed from the following equation using Avogadro’s number (NA = 6.022×1023 atoms or molecules per mole):
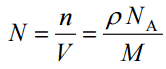
Since nucleons (protons and neutrons) make up most of the mass of ordinary atoms, the density of normal matter tends to be limited by how closely we can pack these nucleons and depends on the internal atomic structure of a substance. The densest material found on earth is the metal osmium, but its density pales by comparison to the densities of exotic astronomical objects such as white dwarf stars and neutron stars.
If we include man made elements, the densest so far is Hassium. Hassium is a chemical element with symbol Hs and atomic number 108. It is a synthetic element (first synthesised at Hasse in Germany) and radioactive. The most stable known isotope, 269Hs, has a half-life of approximately 9.7 seconds. It has an estimated density of 40.7 x 103 kg/m3. The density of Hassium results from its high atomic weight and from the significant decrease in ionic radii of the elements in the lanthanide series, known as lanthanide and actinide contraction.
–