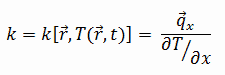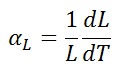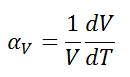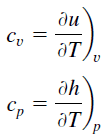Hydrogen
Nonmetals
Helium
Noble gas
Lithium
Alkali metal
Beryllium
Alkaline earth metal
Boron
Metalloids
Carbon
Nonmetals
Nitrogen
Nonmetals
Oxygen
Nonmetals
Fluorine
Nonmetals
Neon
Noble gas
Sodium
Alkali metal
Magnesium
Alkaline earth metal
Aluminium
Post-transition metals
Silicon
Metalloids
Phosphorus
Nonmetal
Sulfur
Nonmetal
Chlorine
Nonmetal
Argon
Noble gas
Potassium
Alkali metal
Calcium
Alkaline earth metal
Scandium
Transition metals
Titanium
Transition metals
Vanadium
Transition metals
Chromium
Transition metals
Manganese
Transition metals
Iron
Transition metals
Cobalt
Transition metals
Nickel
Transition metals
Copper
Transition metals
Zinc
Transition metals
Gallium
Post-transition metals
Germanium
Metalloids
Arsenic
Metalloids
Selenium
Nonmetal
Bromine
Nonmetal
Krypton
Noble gas
Rubidium
Alkali metals
Strontium
Alkaline earth metals
Yttrium
Transition metals
Zirconium
Transition metals
Niobium
Transition metals
Molybdenum
Transition metals
Technetium
Transition metals
Ruthenium
Transition metals
Rhodium
Transition metals
Palladium
Transition metals
Silver
Transition metals
Cadmium
Transition metals
Indium
Post-transition metals
Tin
Post-transition metals
Antimony
Metalloids
Tellurium
Metalloids
Iodine
Nonmetal
Xenon
Noble gas
Caesium
Alkali metals
Lanthanoids
Hafnium
Transition metals
Tantalum
Transition metals
Tungsten
Transition metals
Rhenium
Transition metals
Osmium
Transition metals
Iridium
Transition metals
Platinum
Transition metals
Gold
Transition metals
Mercury
Transition metals
Thallium
Post-transition metals
Lead
Post-transition metals
Bismuth
Post-transition metals
Polonium
Post-transition metals
Astatine
Metalloids
Radon
Noble gas
Francium
Alkali metal
Radium
Alkaline earth metal
Actinoids
Rutherfordium
Transition metal
Dubnium
Transition metal
Seaborgium
Transition metal
Bohrium
Transition metal
Hassium
Transition metal
Meitnerium
Darmstadtium
Roentgenium
Copernicium
Nihonium
Flerovium
Moscovium
Livermorium
Tennessine
Oganesson
Lanthanum
Lanthanoids
Cerium
Lanthanoids
Praseodymium
Lanthanoids
Neodymium
Lanthanoids
Promethium
Lanthanoids
Samarium
Lanthanoids
Europium
Lanthanoids
Gadolinium
Lanthanoids
Terbium
Lanthanoids
Dysprosium
Lanthanoids
Holmium
Lanthanoids
Erbium
Lanthanoids
Thulium
Lanthanoids
Ytterbium
Lanthanoids
Lutetium
Lanthanoids
Actinium
Actinoids
Thorium
Actinoids
Protactinium
Actinoids
Uranium
Actinoids
Neptunium
Actinoids
Plutonium
Actinoids
Americium
Actinoids
Curium
Actinoids
Berkelium
Actinoids
Californium
Actinoids
Einsteinium
Actinoids
Fermium
Actinoids
Mendelevium
Actinoids
Nobelium
Actinoids
Lawrencium
Actinoids
What is Uranium
Uranium is a chemical element with atomic number 92 which means there are 92 protons and 92 electrons in the atomic structure. The chemical symbol for Uranium is U.
Uranium is a silvery-white metal in the actinide series of the periodic table. Uranium is weakly radioactive because all isotopes of uranium are unstable, with half-lives varying between 159,200 years and 4.5 billion years. Uranium has the highest atomic weight of the primordially occurring elements. Its density is about 70% higher than that of lead, and slightly lower than that of gold or tungsten. Uranium is commonly found at low levels (a few ppm – parts per million) in all rocks, soil, water, plants, and animals (including humans). Uranium occurs also in seawater, and can be recovered from the ocean water. Significant concentrations of uranium occur in some substances such as uraninite (the most common uranium ore), phosphate rock deposits, and other minerals.
Uranium – Properties
| Element | Uranium |
|---|---|
| Atomic Number | 92 |
| Symbol | U |
| Element Category | Rare Earth Metal |
| Phase at STP | Solid |
| Atomic Mass [amu] | 238.0289 |
| Density at STP [g/cm3] | 19.05 |
| Electron Configuration | [Rn] 5f3 6d1 7s2 |
| Possible Oxidation States | +3,4,5,6 |
| Electron Affinity [kJ/mol] | — |
| Electronegativity [Pauling scale] | 1.38 |
| 1st Ionization Energy [eV] | 6.1941 |
| Year of Discovery | 1789 |
| Discoverer | Klaproth, Martin Heinrich |
| Thermal properties | |
| Melting Point [Celsius scale] | 1132 |
| Boiling Point [Celsius scale] | 4131 |
| Thermal Expansion µm/(m·K) | 13.9 |
| Thermal Conductivity [W/m K] | 27 |
| Specific Heat [J/g K] | 0.12 |
| Heat of Fusion [kJ/mol] | 8.52 |
| Heat of Vaporization [kJ/mol] | 417 |
Atomic Number of Uranium
Uranium is a chemical element with atomic number 92 which means there are 92 protons and 92 electrons in the atomic structure. The chemical symbol for Uranium is U.
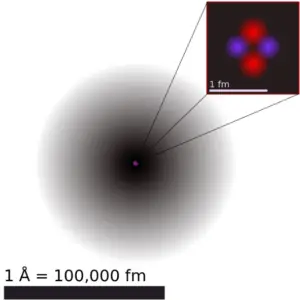
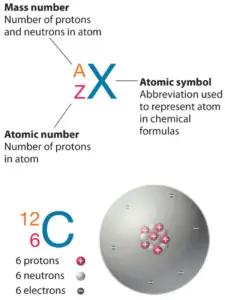 The atom consist of a small but massive nucleus surrounded by a cloud of rapidly moving electrons. The nucleus is composed of protons and neutrons. Total number of protons in the nucleus is called the atomic number of the atom and is given the symbol Z. The total electrical charge of the nucleus is therefore +Ze, where e (elementary charge) equals to 1,602 x 10-19 coulombs. In a neutral atom there are as many electrons as protons moving about nucleus. It is the electrons that are responsible for the chemical bavavior of atoms, and which identify the various chemical elements.
The atom consist of a small but massive nucleus surrounded by a cloud of rapidly moving electrons. The nucleus is composed of protons and neutrons. Total number of protons in the nucleus is called the atomic number of the atom and is given the symbol Z. The total electrical charge of the nucleus is therefore +Ze, where e (elementary charge) equals to 1,602 x 10-19 coulombs. In a neutral atom there are as many electrons as protons moving about nucleus. It is the electrons that are responsible for the chemical bavavior of atoms, and which identify the various chemical elements.
See also: Atomic Number – Does it conserve in a nuclear reaction?
Atomic Number and Chemical Properties
Every solid, liquid, gas, and plasma is composed of neutral or ionized atoms. The chemical properties of the atom are determined by the number of protons, in fact, by number and arrangement of electrons. The configuration of these electrons follows from the principles of quantum mechanics. The number of electrons in each element’s electron shells, particularly the outermost valence shell, is the primary factor in determining its chemical bonding behavior. In the periodic table, the elements are listed in order of increasing atomic number Z.
It is the Pauli exclusion principle that requires the electrons in an atom to occupy different energy levels instead of them all condensing in the ground state. The ordering of the electrons in the ground state of multielectron atoms, starts with the lowest energy state (ground state) and moves progressively from there up the energy scale until each of the atom’s electrons has been assigned a unique set of quantum numbers. This fact has key implications for the building up of the periodic table of elements.
Neutron Number and Mass Number of Uranium
Mass numbers of typical isotopes of Uranium are 238, 235.
The total number of neutrons in the nucleus of an atom is called the neutron number of the atom and is given the symbol N. Neutron number plus atomic number equals atomic mass number: N+Z=A. The difference between the neutron number and the atomic number is known as the neutron excess: D = N – Z = A – 2Z.
Neutron number is rarely written explicitly in nuclide symbol notation, but appears as a subscript to the right of the element symbol. Nuclides that have the same neutron number but a different proton number are called isotones. The various species of atoms whose nuclei contain particular numbers of protons and neutrons are called nuclides. Each nuclide is denoted by chemical symbol of the element (this specifies Z) with tha atomic mass number as supescript. Therefore, we cannot determine the neutron number of uranium, for example. We can determine the neutron number of certain isotope. For example, the neutron number of uranium-238 is 238-92=146.
Neutron and Mass Numbers and Nuclear Properties
Properties of atomic nuclei (atomic mass, nuclear cross-sections) are determined by the number of protons and number of neutrons (neutron number). It must be noted, especially nuclear cross-sections may vary by many orders from nuclide with the neutron number N to nuclide with the neutron number N+1. For example, actinides with odd neutron number are usually fissile (fissionable with slow neutrons) while actinides with even neutron number are usually not fissile (but are fissionable with fast neutrons). Heavy nuclei with an even number of protons and an even number of neutrons are (due to Pauli exclusion principle) very stable thanks to the occurrence of ‘paired spin’. On the other hand, nuclei with an odd number of protons and neutrons are mostly unstable.
Neutron and Atomic Numbers and Nuclear Stability
Nuclear stability is a concept that helps to identify the stability of an isotope. To identify the stability of an isotope it is needed to find the ratio of neutrons to protons. To determine the stability of an isotope you can use the ratio neutron/proton (N/Z). Also to help understand this concept there is a chart of the nuclides, known as a Segre chart. This chart shows a plot of the known nuclides as a function of their atomic and neutron numbers. It can be observed from the chart that there are more neutrons than protons in nuclides with Z greater than about 20 (Calcium). These extra neutrons are necessary for stability of the heavier nuclei. The excess neutrons act somewhat like nuclear glue. Only two stable nuclides have fewer neutrons than protons: hydrogen-1 and helium-3.
Atomic nuclei consist of protons and neutrons, which attract each other through the nuclear force, while protons repel each other via the electric force due to their positive charge. These two forces compete, leading to various stability of nuclei. There are only certain combinations of neutrons and protons, which forms stable nuclei.
Neutrons stabilize the nucleus, because they attract each other and protons , which helps offset the electrical repulsion between protons. As a result, as the number of protons increases, an increasing ratio of neutrons to protons is needed to form a stable nucleus. If there are too many or too few neutrons for a given number of protons, the resulting nucleus is not stable and it undergoes radioactive decay. Unstable isotopes decay through various radioactive decay pathways, most commonly alpha decay, beta decay, gamma decay or electron capture. Many other rare types of decay, such as spontaneous fission or neutron emission are known.
Atomic Mass of Uranium
Atomic mass of Uranium is 238.0289 u.
The atomic mass is the mass of an atom. The atomic mass or relative isotopic mass refers to the mass of a single particle, and therefore is tied to a certain specific isotope of an element. The atomic mass is carried by the atomic nucleus, which occupies only about 10-12 of the total volume of the atom or less, but it contains all the positive charge and at least 99.95% of the total mass of the atom. Note that, each element may contain more isotopes, therefore this resulting atomic mass is calculated from naturally-occuring isotopes and their abundance.
The size and mass of atoms are so small that the use of normal measuring units, while possible, is often inconvenient. Units of measure have been defined for mass and energy on the atomic scale to make measurements more convenient to express. The unit of measure for mass is the atomic mass unit (amu). One atomic mass unit is equal to 1.66 x 10-24 grams. One unified atomic mass unit is approximately the mass of one nucleon (either a single proton or neutron) and is numerically equivalent to 1 g/mol.
For 12C the atomic mass is exactly 12u, since the atomic mass unit is defined from it. For other isotopes, the isotopic mass usually differs and is usually within 0.1 u of the mass number. For example, 63Cu (29 protons and 34 neutrons) has a mass number of 63 and an isotopic mass in its nuclear ground state is 62.91367 u.
There are two reasons for the difference between mass number and isotopic mass, known as the mass defect:
- The neutron is slightly heavier than the proton. This increases the mass of nuclei with more neutrons than protons relative to the atomic mass unit scale based on 12C with equal numbers of protons and neutrons.
- The nuclear binding energy varies between nuclei. A nucleus with greater binding energy has a lower total energy, and therefore a lower mass according to Einstein’s mass-energy equivalence relation E = mc2. For 63Cu the atomic mass is less than 63 so this must be the dominant factor.
Note that, it was found the rest mass of an atomic nucleus is measurably smaller than the sum of the rest masses of its constituent protons, neutrons and electrons. Mass was no longer considered unchangeable in the closed system. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E=mc2), this binding energy is proportional to this mass difference and it is known as the mass defect.
See also: Atomic Mass Number – Does it conserve in a nuclear reaction?
Atomic Radius of Uranium
The atomic radius of Uranium atom is 196pm (covalent radius).
It must be noted, atoms lack a well-defined outer boundary. The atomic radius of a chemical element is a measure of the distance out to which the electron cloud extends from the nucleus. However, this assumes the atom to exhibit a spherical shape, which is only obeyed for atoms in vacuum or free space. Therefore, there are various non-equivalent definitions of atomic radius.
- Van der Waals radius. In principle, Vana der Waals radius is half the minimum distance between the nuclei of two atoms of the element that are not bound to the same molecule.
- Ionic radius. An ionic radius is one-half the distance between the nuclei of two ions in an ionic bond.
- Covalent radius. Covalent radius is the nominal radius of the atoms of an element when covalently bound to other atoms.
- Metallic radius. A metallic radius is one-half the distance between the nuclei of two adjacent atoms in a crystalline structure, when joined to other atoms by metallic bonds.
On the periodic table of the elements, atomic radius tends to increase when moving down columns, but decrease when moving across rows (left to right). Consequently, the smallest atom is helium with a radius of 32 pm, while one of the largest is caesium at 225 pm. The atomic radii decrease across the periodic table because as the atomic number increases, the number of protons increases across the period, but the extra electrons are only added to the same quantum shell. Therefore, the effective nuclear charge towards the outermost electrons increases, drawing the outermost electrons closer. As a result, the electron cloud contracts and the atomic radius decreases.
 The volume of an atom is about 15 orders of magnitude larger than the volume of a nucleus. For uranium atom, the Van der Waals radius is about 186 pm = 1.86 ×10−10m. The Van der Waals radius, rw, of an atom is the radius of an imaginary hard sphere representing the distance of closest approach for another atom. Assuming spherical shape, the uranium atom have volume of about 26.9 ×10−30 m3. But this “huge” space is occupied primarily by electrons, because the nucleus occupies only about 1721×10−45 m3 of space. These electrons together weigh only a fraction (let say 0.05%) of entire atom.
The volume of an atom is about 15 orders of magnitude larger than the volume of a nucleus. For uranium atom, the Van der Waals radius is about 186 pm = 1.86 ×10−10m. The Van der Waals radius, rw, of an atom is the radius of an imaginary hard sphere representing the distance of closest approach for another atom. Assuming spherical shape, the uranium atom have volume of about 26.9 ×10−30 m3. But this “huge” space is occupied primarily by electrons, because the nucleus occupies only about 1721×10−45 m3 of space. These electrons together weigh only a fraction (let say 0.05%) of entire atom.
It may seem, that the space and in fact the matter is empty, but it is not. Due to the quantum nature of electrons, the electrons are not point particles, they are smeared out over the whole atom. The classical description cannot be used to describe things on the atomic scale. On the atomic scale, physicists have found that quantum mechanics describes things very well on that scale. Particle locations in quantum mechanics are not at an exact position, they are described by a probability density function. Therefore the space in an atom (between electrons and an atomic nucleus) is not empty, but it is filled by a probability density function of electrons (usually known as “electron cloud“).
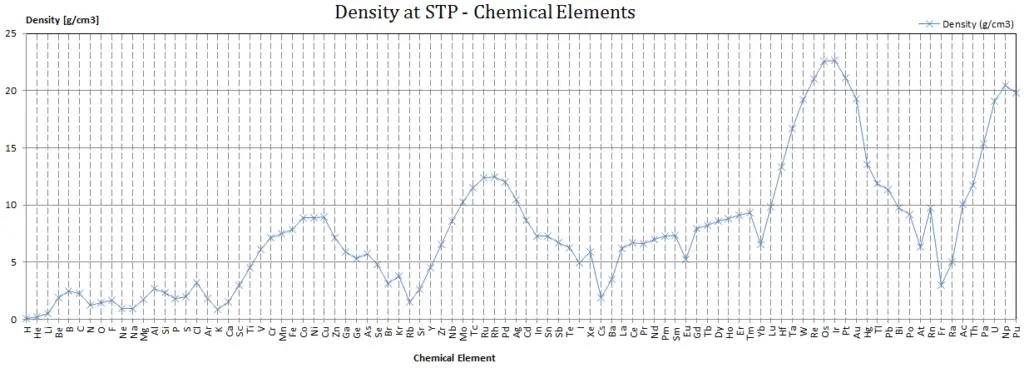
 Density of Uranium
Density of Uranium
Density of Uranium is 19.05g/cm3.
Typical densities of various substances are at atmospheric pressure.
Density is defined as the mass per unit volume. It is an intensive property, which is mathematically defined as mass divided by volume:
ρ = m/V
In words, the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance. The standard SI unit is kilograms per cubic meter (kg/m3). The Standard English unit is pounds mass per cubic foot (lbm/ft3).
Density – Atomic Mass and Atomic Number Density
Since the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance, it is obvious, the density of a substance strongly depends on its atomic mass and also on the atomic number density (N; atoms/cm3),
- Atomic Weight. The atomic mass is carried by the atomic nucleus, which occupies only about 10-12 of the total volume of the atom or less, but it contains all the positive charge and at least 99.95% of the total mass of the atom. Therefore it is determined by the mass number (number of protons and neutrons).
- Atomic Number Density. The atomic number density (N; atoms/cm3), which is associated with atomic radii, is the number of atoms of a given type per unit volume (V; cm3) of the material. The atomic number density (N; atoms/cm3) of a pure material having atomic or molecular weight (M; grams/mol) and the material density (⍴; gram/cm3) is easily computed from the following equation using Avogadro’s number (NA = 6.022×1023 atoms or molecules per mole):
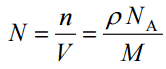
Since nucleons (protons and neutrons) make up most of the mass of ordinary atoms, the density of normal matter tends to be limited by how closely we can pack these nucleons and depends on the internal atomic structure of a substance. The densest material found on earth is the metal osmium, but its density pales by comparison to the densities of exotic astronomical objects such as white dwarf stars and neutron stars.
If we include man made elements, the densest so far is Hassium. Hassium is a chemical element with symbol Hs and atomic number 108. It is a synthetic element (first synthesised at Hasse in Germany) and radioactive. The most stable known isotope, 269Hs, has a half-life of approximately 9.7 seconds. It has an estimated density of 40.7 x 103 kg/m3. The density of Hassium results from its high atomic weight and from the significant decrease in ionic radii of the elements in the lanthanide series, known as lanthanide and actinide contraction.
Density – Pressure and Temperature
The density of a material varies with temperature and pressure. This variation is typically small for solids and liquids but much greater for gases. Most materials expand when their temperatures increase. Rising temperatures make the liquid expand in a liquid-in-tube thermometer and bend bimetallic strips. As a result of this expansion, the density of most materials decreases. This effect is caused by a decrease in the atomic number density. This dependence is usually expressed by the coefficient of linear or volume expansion.
Increasing the pressure on an material (especially for liquids or gases) decreases the volume of the object and thus increases its density via the atomic number density. Compressibility (also known as the coefficient of compressibility is a measure of the relative volume change of a fluid or solid as a response to a pressure (or mean stress) change.
See also: What is Density
See also: Densest Materials of the Earth
Electron Configuration and Oxidation States of Uranium
Electron configuration of Uranium is [Rn] 5f3 6d1 7s2.
Possible oxidation states are +3,4,5,6.
Electron Configuration
The periodic table is a tabular display of the chemical elements organized on the basis of their atomic numbers, electron configurations, and chemical properties. The electron configuration is the distribution of electrons of an atom or molecule (or other physical structure) in atomic or molecular orbitals. Knowledge of the electron configuration of different atoms is useful in understanding the structure of the periodic table of elements.
Every solid, liquid, gas, and plasma is composed of neutral or ionized atoms. The chemical properties of the atom are determined by the number of protons, in fact, by number and arrangement of electrons. The configuration of these electrons follows from the principles of quantum mechanics. The number of electrons in each element’s electron shells, particularly the outermost valence shell, is the primary factor in determining its chemical bonding behavior. In the periodic table, the elements are listed in order of increasing atomic number Z.
It is the Pauli exclusion principle that requires the electrons in an atom to occupy different energy levels instead of them all condensing in the ground state. The ordering of the electrons in the ground state of multielectron atoms, starts with the lowest energy state (ground state) and moves progressively from there up the energy scale until each of the atom’s electrons has been assigned a unique set of quantum numbers. This fact has key implications for the building up of the periodic table of elements.
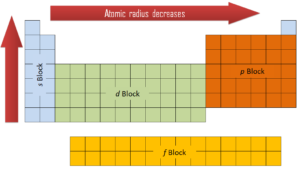
 The first two columns on the left side of the periodic table are where the s subshells are being occupied. Because of this, the first two rows of the periodic table are labeled the s block. Similarly, the p block are the right-most six columns of the periodic table, the d block is the middle 10 columns of the periodic table, while the f block is the 14-column section that is normally depicted as detached from the main body of the periodic table. It could be part of the main body, but then the periodic table would be rather long and cumbersome.
The first two columns on the left side of the periodic table are where the s subshells are being occupied. Because of this, the first two rows of the periodic table are labeled the s block. Similarly, the p block are the right-most six columns of the periodic table, the d block is the middle 10 columns of the periodic table, while the f block is the 14-column section that is normally depicted as detached from the main body of the periodic table. It could be part of the main body, but then the periodic table would be rather long and cumbersome.
For atoms with many electrons, this notation can become lengthy and so an abbreviated notation is used. The electron configuration can be visualized as the core electrons, equivalent to the noble gas of the preceding period, and the valence electrons (e.g. [Xe] 6s2 for barium).
Oxidation States
Oxidation states are typically represented by integers which may be positive, zero, or negative. Most elements have more than one possible oxidation state. For example, carbon has nine possible integer oxidation states from −4 to +4.
The current IUPAC Gold Book definition of oxidation state is:
“Oxidation state of an atom is the charge of this atom after ionic approximation of its heteronuclear bonds…”
and the term oxidation number is nearly synonymous. An element that is not combined with any other different elements has an oxidation state of 0. Oxidation state 0 occurs for all elements – it is simply the element in its elemental form. An atom of an element in a compound will have a positive oxidation state if it has had electrons removed. Similarly, adding electrons results in a negative oxidation state. We have also distinguish between the possible and common oxidation states of every element. For example, silicon has nine possible integer oxidation states from −4 to +4, but only -4, 0 and +4 are common oxidation states.
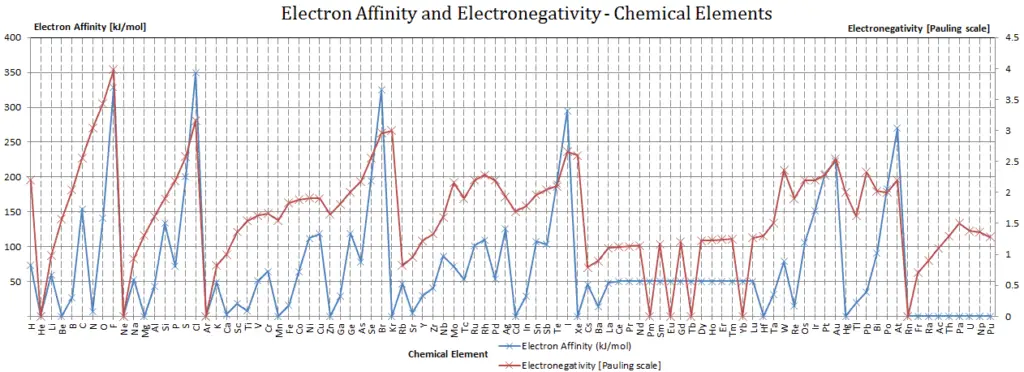
Electron Affinity and Electronegativity of Uranium
Electron affinity of Uranium is — kJ/mol.
Electronegativity of Uranium is 1.38.
Electron Affinity
In chemistry and atomic physics, the electron affinity of an atom or molecule is defined as:
the change in energy (in kJ/mole) of a neutral atom or molecule (in the gaseous phase) when an electron is added to the atom to form a negative ion.
X + e– → X– + energy Affinity = – ∆H
In other words, it can be expressed as the neutral atom’s likelihood of gaining an electron. Note that, ionization energies measure the tendency of a neutral atom to resist the loss of electrons. Electron affinities are more difficult to measure than ionization energies.
An atom of Uranium in the gas phase, for example, gives off energy when it gains an electron to form an ion of Uranium.
U + e– → U– – ∆H = Affinity = — kJ/mol
To use electron affinities properly, it is essential to keep track of sign. When an electron is added to a neutral atom, energy is released. This affinity is known as the first electron affinity and these energies are negative. By convention, the negative sign shows a release of energy. However, more energy is required to add an electron to a negative ion which overwhelms any the release of energy from the electron attachment process. This affinity is known as the second electron affinity and these energies are positive.
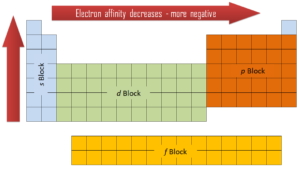 Electron affinity can be either positive or negative value. The greater the negative value, the more stable the anion is. Although affinity varies greatly across the periodic table, some patterns emerge. Generally, the elements on the right side of the periodic table will have large negative electron affinity. The electron affinities will become less negative as you go from the top to the bottom of the periodic table. However, nitrogen, oxygen, and fluorine do not follow this trend. Moreover, nonmetals have more positive affinity than metals. Atoms whose anions are more stable than neutral atoms have a greater affinity. Chlorine most strongly attracts extra electrons, while neon most weakly attracts an extra electron.
Electron affinity can be either positive or negative value. The greater the negative value, the more stable the anion is. Although affinity varies greatly across the periodic table, some patterns emerge. Generally, the elements on the right side of the periodic table will have large negative electron affinity. The electron affinities will become less negative as you go from the top to the bottom of the periodic table. However, nitrogen, oxygen, and fluorine do not follow this trend. Moreover, nonmetals have more positive affinity than metals. Atoms whose anions are more stable than neutral atoms have a greater affinity. Chlorine most strongly attracts extra electrons, while neon most weakly attracts an extra electron.
Affinities of Non metals vs. Affinities of Metals
- Metals: Metals like to lose valence electrons to form cations to have a fully stable shell. The electron affinity of metals is lower than that of nonmetals. Mercury most weakly attracts an extra electron.
- Nonmetals: Generally, nonmetals have more positive electron affinity than metals. Nonmetals like to gain electrons to form anions to have a fully stable electron shell. Chlorine most strongly attracts extra electrons. The electron affinities of the noble gases have not been conclusively measured, so they may or may not have slightly negative values.
Electronegativity
Electronegativity, symbol χ, is a chemical property that describes the tendency of an atom to attract electrons towards this atom. For this purposes, a dimensionless quantity the Pauling scale, symbol χ, is the most commonly used.
The electronegativity of Uranium is: χ = 1.38
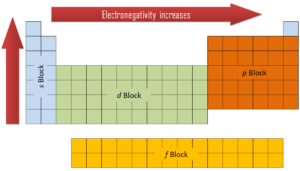 In general, an atom’s electronegativity is affected by both its atomic number and the distance at which its valence electrons reside from the charged nucleus. The higher the associated electronegativity number, the more an element or compound attracts electrons towards it. The most electronegative atom, fluorine, is assigned a value of 4.0, and values range down to cesium and francium which are the least electronegative at 0.7. Electronegativity is related with ionization energy and electron affinity. Electrons with low ionization energies have low electronegativities because their nuclei do not exert a strong attractive force on electrons. Elements with high ionization energies have high electronegativities due to the strong pull exerted by the positive nucleus on the negative electrons. Therefore the electronegativity is greatest at the top-right of the periodic table and decreases toward the bottom-left.
In general, an atom’s electronegativity is affected by both its atomic number and the distance at which its valence electrons reside from the charged nucleus. The higher the associated electronegativity number, the more an element or compound attracts electrons towards it. The most electronegative atom, fluorine, is assigned a value of 4.0, and values range down to cesium and francium which are the least electronegative at 0.7. Electronegativity is related with ionization energy and electron affinity. Electrons with low ionization energies have low electronegativities because their nuclei do not exert a strong attractive force on electrons. Elements with high ionization energies have high electronegativities due to the strong pull exerted by the positive nucleus on the negative electrons. Therefore the electronegativity is greatest at the top-right of the periodic table and decreases toward the bottom-left.
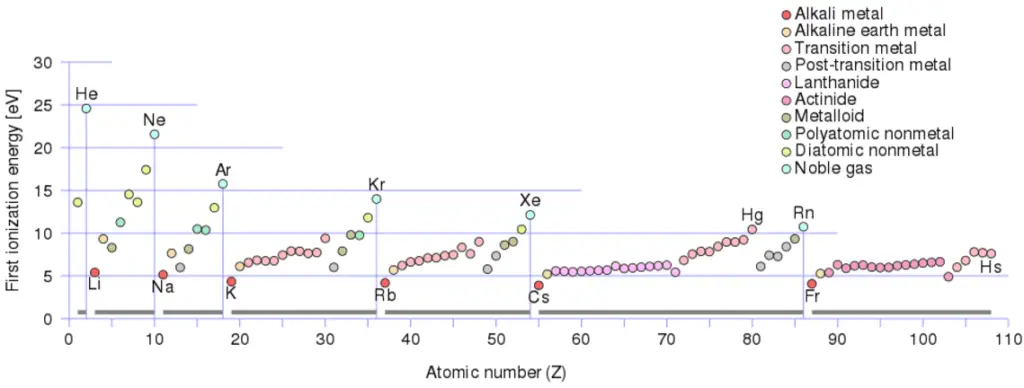
First Ionization Energy of Uranium
First Ionization Energy of Uranium is 6.1941 eV.
Ionization energy, also called ionization potential, is the energy necessary to remove an electron from the neutral atom.
X + energy → X+ + e−
where X is any atom or molecule capable of being ionized, X+ is that atom or molecule with an electron removed (positive ion), and e− is the removed electron.
A Uranium atom, for example, requires the following ionization energy to remove the outermost electron.
U + IE → U+ + e− IE = 6.1941 eV
The ionization energy associated with removal of the first electron is most commonly used. The nth ionization energy refers to the amount of energy required to remove an electron from the species with a charge of (n-1).
1st ionization energy
X → X+ + e−
2nd ionization energy
X+ → X2+ + e−
3rd ionization energy
X2+ → X3+ + e−
Ionization Energy for different Elements
There is an ionization energy for each successive electron removed. The electrons that circle the nucleus move in fairly well-defined orbits. Some of these electrons are more tightly bound in the atom than others. For example, only 7.38 eV is required to remove the outermost electron from a lead atom, while 88,000 eV is required to remove the innermost electron. Helps to understand reactivity of elements (especially metals, which lose electrons).
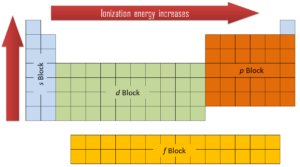 In general, the ionization energy increases moving up a group and moving left to right across a period. Ionization energy is is related with electronegativity and electron affinity. Electrons with low ionization energies have low electronegativities because their nuclei do not exert a strong attractive force on electrons. Elements with high ionization energies have high electronegativities due to the strong pull exerted by the positive nucleus on the negative electrons. Therefore the electronegativity is greatest at the top-right of the periodic table and decreases toward the bottom-left. Moreover:
In general, the ionization energy increases moving up a group and moving left to right across a period. Ionization energy is is related with electronegativity and electron affinity. Electrons with low ionization energies have low electronegativities because their nuclei do not exert a strong attractive force on electrons. Elements with high ionization energies have high electronegativities due to the strong pull exerted by the positive nucleus on the negative electrons. Therefore the electronegativity is greatest at the top-right of the periodic table and decreases toward the bottom-left. Moreover:
- Ionization energy is lowest for the alkali metals which have a single electron outside a closed shell.
- Ionization energy increases across a row on the periodic maximum for the noble gases which have closed shells.
For example, sodium requires only 496 kJ/mol or 5.14 eV/atom to ionize it. On the other hand neon, the noble gas, immediately preceding it in the periodic table, requires 2081 kJ/mol or 21.56 eV/atom.
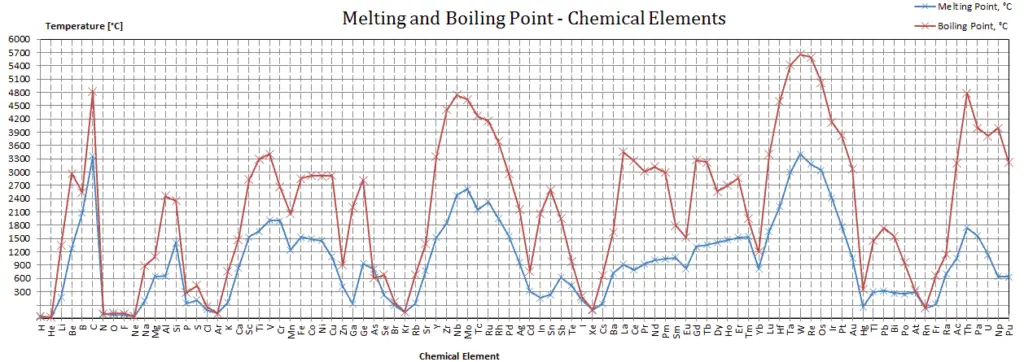
Uranium – Melting Point and Boiling Point
Melting point of Uranium is 1132°C.
Boiling point of Uranium is 4131°C.
Note that, these points are associated with the standard atmospheric pressure.
Boiling Point
In general, boiling is a phase change of a substance from the liquid to the gas phase. The boiling point of a substance is the temperature at which this phase change (boiling or vaporization) occurs. The temperature at which vaporization (boiling) starts to occur for a given pressure is also known as the saturation temperature and at this conditions a mixture of vapor and liquid can exist together. The liquid can be said to be saturated with thermal energy. Any addition of thermal energy results in a phase transition. At the boiling point the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas above the gaseous form is preferred. The pressure at which vaporization (boiling) starts to occur for a given temperature is called the saturation pressure. When considered as the temperature of the reverse change from vapor to liquid, it is referred to as the condensation point.
As can be seen, the boiling point of a liquid varies depending upon the surrounding environmental pressure. A liquid in a partial vacuum has a lower boiling point than when that liquid is at atmospheric pressure. A liquid at high pressure has a higher boiling point than when that liquid is at atmospheric pressure. For example, water boils at 100°C (212°F) at sea level, but at 93.4°C (200.1°F) at 1900 metres (6,233 ft) altitude. On the other hand, water boils at 350°C (662°F) at 16.5 MPa (typical pressure of PWRs).
In the periodic table of elements, the element with the lowest boiling point is helium. Both the boiling points of rhenium and tungsten exceed 5000 K at standard pressure. Since it is difficult to measure extreme temperatures precisely without bias, both have been cited in the literature as having the higher boiling point.
Melting Point
In general, melting is a phase change of a substance from the solid to the liquid phase. The melting point of a substance is the temperature at which this phase change occurs. The melting point also defines a condition in which the solid and liquid can exist in equilibrium. Adding a heat will convert the solid into a liquid with no temperature change. At the melting point the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the melting point, the solid is the more stable state of the two, whereas above the liquid form is preferred. The melting point of a substance depends on pressure and is usually specified at standard pressure. When considered as the temperature of the reverse change from liquid to solid, it is referred to as the freezing point or crystallization point.
See also: Melting Point Depression
The first theory explaining mechanism of melting in the bulk was proposed by Lindemann, who used vibration of atoms in the crystal to explain the melting transition. Solids are similar to liquids in that both are condensed states, with particles that are far closer together than those of a gas. The atoms in a solid are tightly bound to each other, either in a regular geometric lattice (crystalline solids, which include metals and ordinary ice) or irregularly (an amorphous solid such as common window glass), and are typically low in energy. The motion of individual atoms, ions, or molecules in a solid is restricted to vibrational motion about a fixed point. As a solid is heated, its particles vibrate more rapidly as the solid absorbs kinetic energy. At some point the amplitude of vibration becomes so large that the atoms start to invade the space of their nearest neighbors and disturb them and the melting process initiates. The melting point is the temperature at which the disruptive vibrations of the particles of the solid overcome the attractive forces operating within the solid.
As with boiling points, the melting point of a solid is dependent on the strength of those attractive forces. For example, sodium chloride (NaCl) is an ionic compound that consists of a multitude of strong ionic bonds. Sodium chloride melts at 801°C. On the other hand, ice (solid H2O) is a molecular compound whose molecules are held together by hydrogen bonds, which is effectively a strong example of an interaction between two permanent dipoles. Though hydrogen bonds are the strongest of the intermolecular forces, the strength of hydrogen bonds is much less than that of ionic bonds. The melting point of ice is 0 °C.
Covalent bonds often result in the formation of small collections of better-connected atoms called molecules, which in solids and liquids are bound to other molecules by forces that are often much weaker than the covalent bonds that hold the molecules internally together. Such weak intermolecular bonds give organic molecular substances, such as waxes and oils, their soft bulk character, and their low melting points (in liquids, molecules must cease most structured or oriented contact with each other).
Uranium – Thermal Conductivity
Thermal conductivity of Uranium is 27 W/(m·K).
The heat transfer characteristics of a solid material are measured by a property called the thermal conductivity, k (or λ), measured in W/m.K. It is a measure of a substance’s ability to transfer heat through a material by conduction. Note that Fourier’s law applies for all matter, regardless of its state (solid, liquid, or gas), therefore, it is also defined for liquids and gases.
The thermal conductivity of most liquids and solids varies with temperature. For vapors, it also depends upon pressure. In general:
Most materials are very nearly homogeneous, therefore we can usually write k = k (T). Similar definitions are associated with thermal conductivities in the y- and z-directions (ky, kz), but for an isotropic material the thermal conductivity is independent of the direction of transfer, kx = ky = kz = k.
Thermal Conductivity of Metals
- the migration of free electrons
- lattice vibrational waves (phonons)
When electrons and phonons carry thermal energy leading to conduction heat transfer in a solid, the thermal conductivity may be expressed as:
k = ke + kph
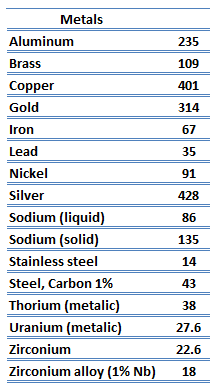 Metals are solids and as such they possess crystalline structure where the ions (nuclei with their surrounding shells of core electrons) occupy translationally equivalent positions in the crystal lattice. Metals in general have high electrical conductivity, high thermal conductivity, and high density. Accordingly, transport of thermal energy may be due to two effects:
Metals are solids and as such they possess crystalline structure where the ions (nuclei with their surrounding shells of core electrons) occupy translationally equivalent positions in the crystal lattice. Metals in general have high electrical conductivity, high thermal conductivity, and high density. Accordingly, transport of thermal energy may be due to two effects:
- the migration of free electrons
- lattice vibrational waves (phonons).
When electrons and phonons carry thermal energy leading to conduction heat transfer in a solid, the thermal conductivity may be expressed as:
k = ke + kph
The unique feature of metals as far as their structure is concerned is the presence of charge carriers, specifically electrons. The electrical and thermal conductivities of metals originate from the fact that their outer electrons are delocalized. Their contribution to the thermal conductivity is referred to as the electronic thermal conductivity, ke. In fact, in pure metals such as gold, silver, copper, and aluminum, the heat current associated with the flow of electrons by far exceeds a small contribution due to the flow of phonons. In contrast, for alloys, the contribution of kph to k is no longer negligible.
Thermal Conductivity of Nonmetals
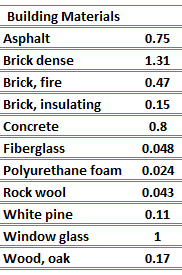 For nonmetallic solids, k is determined primarily by kph, which increases as the frequency of interactions between the atoms and the lattice decreases. In fact, lattice thermal conduction is the dominant thermal conduction mechanism in nonmetals, if not the only one. In solids, atoms vibrate about their equilibrium positions (crystal lattice). The vibrations of atoms are not independent of each other, but are rather strongly coupled with neighboring atoms. The regularity of the lattice arrangement has an important effect on kph, with crystalline (well-ordered) materials like quartz having a higher thermal conductivity than amorphous materials like glass. At sufficiently high temperatures kph ∝ 1/T.
For nonmetallic solids, k is determined primarily by kph, which increases as the frequency of interactions between the atoms and the lattice decreases. In fact, lattice thermal conduction is the dominant thermal conduction mechanism in nonmetals, if not the only one. In solids, atoms vibrate about their equilibrium positions (crystal lattice). The vibrations of atoms are not independent of each other, but are rather strongly coupled with neighboring atoms. The regularity of the lattice arrangement has an important effect on kph, with crystalline (well-ordered) materials like quartz having a higher thermal conductivity than amorphous materials like glass. At sufficiently high temperatures kph ∝ 1/T.
The quanta of the crystal vibrational field are referred to as ‘‘phonons.’’ A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, like solids and some liquids. Phonons play a major role in many of the physical properties of condensed matter, like thermal conductivity and electrical conductivity. In fact, for crystalline, nonmetallic solids such as diamond, kph can be quite large, exceeding values of k associated with good conductors, such as aluminum. In particular, diamond has the highest hardness and thermal conductivity (k = 1000 W/m.K) of any bulk material.
Thermal Conductivity of Liquids and Gases
In physics, a fluid is a substance that continually deforms (flows) under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids. Because the intermolecular spacing is much larger and the motion of the molecules is more random for the fluid state than for the solid state, thermal energy transport is less effective. The thermal conductivity of gases and liquids is therefore generally smaller than that of solids. In liquids, the thermal conduction is caused by atomic or molecular diffusion. In gases, the thermal conduction is caused by diffusion of molecules from higher energy level to the lower level.
Thermal Conductivity of Gases
 The effect of temperature, pressure, and chemical species on the thermal conductivity of a gas may be explained in terms of the kinetic theory of gases. Air and other gases are generally good insulators, in the absence of convection. Therefore, many insulating materials (e.g.polystyrene) function simply by having a large number of gas-filled pockets which prevent large-scale convection. Alternation of gas pocket and solid material causes that the heat must be transferred through many interfaces causing rapid decrease in heat transfer coefficient.
The effect of temperature, pressure, and chemical species on the thermal conductivity of a gas may be explained in terms of the kinetic theory of gases. Air and other gases are generally good insulators, in the absence of convection. Therefore, many insulating materials (e.g.polystyrene) function simply by having a large number of gas-filled pockets which prevent large-scale convection. Alternation of gas pocket and solid material causes that the heat must be transferred through many interfaces causing rapid decrease in heat transfer coefficient.
The thermal conductivity of gases is directly proportional to the density of the gas, the mean molecular speed, and especially to the mean free path of molecule. The mean free path also depends on the diameter of the molecule, with larger molecules more likely to experience collisions than small molecules, which is the average distance traveled by an energy carrier (a molecule) before experiencing a collision. Light gases, such as hydrogen and helium typically have high thermal conductivity. Dense gases such as xenon and dichlorodifluoromethane have low thermal conductivity.
In general, the thermal conductivity of gases increases with increasing temperature.
Thermal Conductivity of Liquids
As was written, in liquids, the thermal conduction is caused by atomic or molecular diffusion, but physical mechanisms for explaining the thermal conductivity of liquids are not well understood. Liquids tend to have better thermal conductivity than gases, and the ability to flow makes a liquid suitable for removing excess heat from mechanical components. The heat can be removed by channeling the liquid through a heat exchanger. The coolants used in nuclear reactors include water or liquid metals, such as sodium or lead.
The thermal conductivity of nonmetallic liquids generally decreases with increasing temperature.
Coefficient of Thermal Expansion of Uranium
Linear thermal expansion coefficient of Uranium is 13.9 µm/(m·K)
Thermal expansion is generally the tendency of matter to change its dimensions in response to a change in temperature. It is usually expressed as a fractional change in length or volume per unit temperature change. Thermal expansion is common for solids, liquids and for gases. Unlike gases or liquids, solid materials tend to keep their shape when undergoing thermal expansion. A linear expansion coefficient is usually employed in describing the expansion of a solid, while a volume expansion coefficient is more useful for a liquid or a gas.
The linear thermal expansion coefficient is defined as:
where L is a particular length measurement and dL/dT is the rate of change of that linear dimension per unit change in temperature.
The volumetric thermal expansion coefficient is the most basic thermal expansion coefficient, and the most relevant for fluids. In general, substances expand or contract when their temperature changes, with expansion or contraction occurring in all directions.
The volumetric thermal expansion coefficient is defined as:
where L is the volume of the material and dV/dT is the rate of change of that volume per unit change in temperature.
In a solid or liquid, there is a dynamic balance between the cohesive forces holding the atoms or molecules together and the conditions created by temperature. Therefore higher temperatures imply greater distance between atoms. Different materials have different bonding forces and therefore different expansion coefficients. If a crystalline solid is isometric (has the same structural configuration throughout), the expansion will be uniform in all dimensions of the crystal. For these materials, the area and volumetric thermal expansion coefficient are, respectively, approximately twice and three times larger than the linear thermal expansion coefficient (αV = 3αL). If it is not isometric, there may be different expansion coefficients for different crystallographic directions, and the crystal will change shape as the temperature changes.
Uranium – Specific Heat, Latent Heat of Fusion, Latent Heat of Vaporization
Specific heat of Uranium is 0.12 J/g K.
Latent Heat of Fusion of Uranium is 8.52 kJ/mol.
Latent Heat of Vaporization of Uranium is 417 kJ/mol.
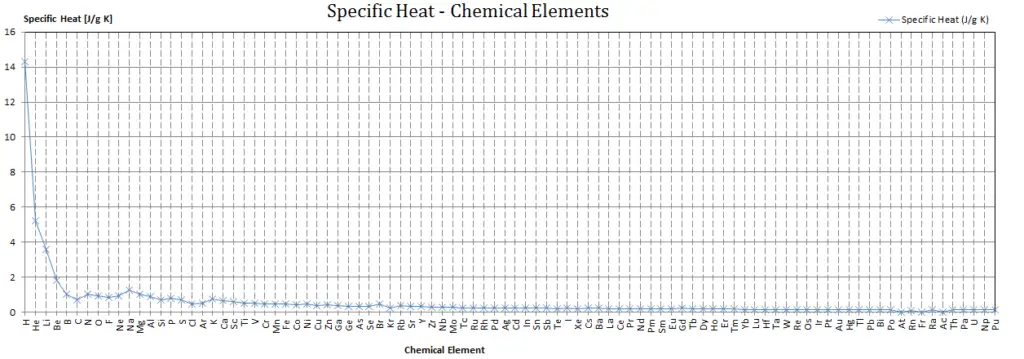
Specific Heat
Specific heat, or specific heat capacity, is a property related to internal energy that is very important in thermodynamics. The intensive properties cv and cp are defined for pure, simple compressible substances as partial derivatives of the internal energy u(T, v) and enthalpy h(T, p), respectively:
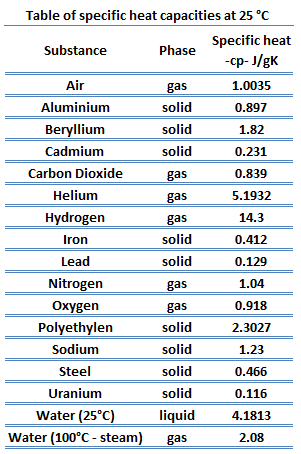 where the subscripts v and p denote the variables held fixed during differentiation. The properties cv and cp are referred to as specific heats(or heat capacities) because under certain special conditions they relate the temperature change of a system to the amount of energy added by heat transfer. Their SI units are J/kg K or J/mol K.
where the subscripts v and p denote the variables held fixed during differentiation. The properties cv and cp are referred to as specific heats(or heat capacities) because under certain special conditions they relate the temperature change of a system to the amount of energy added by heat transfer. Their SI units are J/kg K or J/mol K.
Different substances are affected to different magnitudes by the addition of heat. When a given amount of heat is added to different substances, their temperatures increase by different amounts.
Heat capacity is an extensive property of matter, meaning it is proportional to the size of the system. Heat capacity C has the unit of energy per degree or energy per kelvin. When expressing the same phenomenon as an intensive property, the heat capacity is divided by the amount of substance, mass, or volume, thus the quantity is independent of the size or extent of the sample.
Latent Heat of Vaporization
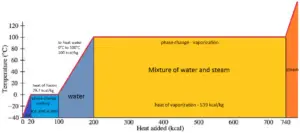 In general, when a material changes phase from solid to liquid, or from liquid to gas a certain amount of energy is involved in this change of phase. In case of liquid to gas phase change, this amount of energy is known as the enthalpy of vaporization, (symbol ∆Hvap; unit: J) also known as the (latent) heat of vaporization or heat of evaporation. As an example, see the figure, which descibes phase transitions of water.
In general, when a material changes phase from solid to liquid, or from liquid to gas a certain amount of energy is involved in this change of phase. In case of liquid to gas phase change, this amount of energy is known as the enthalpy of vaporization, (symbol ∆Hvap; unit: J) also known as the (latent) heat of vaporization or heat of evaporation. As an example, see the figure, which descibes phase transitions of water.
Latent heat is the amount of heat added to or removed from a substance to produce a change in phase. This energy breaks down the intermolecular attractive forces, and also must provide the energy necessary to expand the gas (the pΔV work). When latent heat is added, no temperature change occurs. The enthalpy of vaporization is a function of the pressure at which that transformation takes place.
The temperature at which vaporization (boiling) starts to occur for a given pressure is also known as the saturation temperature and at this conditions a mixture of vapor and liquid can exist together. The liquid can be said to be saturated with thermal energy. Any addition of thermal energy results in a phase transition. At the boiling point the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas above the gaseous form is preferred.
Latent Heat of Fusion
In case of solid to liquid phase change, the change in enthalpy required to change its state is known as the enthalpy of fusion, (symbol ∆Hfus; unit: J) also known as the (latent) heat of fusion. Latent heat is the amount of heat added to or removed from a substance to produce a change in phase. This energy breaks down the intermolecular attractive forces, and also must provide the energy necessary to expand the system (the pΔV work).
The liquid phase has a higher internal energy than the solid phase. This means energy must be supplied to a solid in order to melt it and energy is released from a liquid when it freezes, because the molecules in the liquid experience weaker intermolecular forces and so have a higher potential energy (a kind of bond-dissociation energy for intermolecular forces).
The temperature at which the phase transition occurs is the melting point. The melting point also defines a condition in which the solid and liquid can exist in equilibrium. Adding a heat will convert the solid into a liquid with no temperature change. At the melting point the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the melting point, the solid is the more stable state of the two, whereas above the liquid form is preferred. The melting point of a substance depends on pressure and is usually specified at standard pressure. When considered as the temperature of the reverse change from liquid to solid, it is referred to as the freezing point or crystallization point.
Uranium – Electrical Resistivity and Electrical Conductivity
Electrical resistivity of Uranium is 280 nΩ·m.
Electrical resistivity and its converse, electrical conductivity, is a fundamental property of a material that quantifies how strongly it resists or conducts the flow of electric current. A low resistivity indicates a material that readily allows the flow of electric current. The symbol of resistivity is usually the Greek letter ρ (rho). The SI unit of electrical resistivity is the ohm-metre (Ω⋅m). Note that, electrical resistivity is not the same as electrical resistance. Electrical resistance is expressed in Ohms. While resistivity is a material property, resistance is the property of an object.
Conductors – Semiconductors – Resistors
Substances in which electricity can flow are called conductors. Conductors are made of high-conductivity materials such as metals, in particular copper and aluminium.
Insulators, on the other hand, are made of a wide variety of materials depending on factors such as the desired resistance.
Semiconductors are materials, inorganic or organic, which have the ability to control their conduction depending on chemical structure, temperature, illumination, and presence of dopants. The name semiconductor comes from the fact that these materials have an electrical conductivity between that of a metal, like copper, gold, etc. and an insulator, such as glass. They have an energy gap less than 4eV (about 1eV). In solid-state physics, this energy gap or band gap is an energy range between valence band and conduction band where electron states are forbidden. In contrast to conductors, electrons in a semiconductor must obtain energy (e.g. from ionizing radiation) to cross the band gap and to reach the conduction band.
To understand the difference between metals, semiconductors and electrical insulators, we have to define the following terms from solid-state physics:
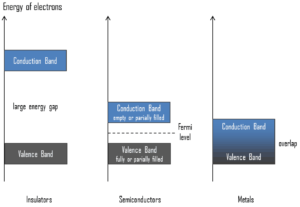 Valence Band. In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level and thus determine the electrical conductivity of the solid. In electrical insulators and semiconductors, the valence band is the highest range of electron energies in which electrons are normally present at absolute zero temperature. For example, a silicon atom has fourteen electrons. In the ground state, they are arranged in the electron configuration [Ne]3s23p2. Of these, four are valence electrons, occupying the 3s orbital and two of the 3p orbitals. The distinction between the valence and conduction bands is meaningless in metals, because conduction occurs in one or more partially filled bands that take on the properties of both the valence and conduction bands.
Valence Band. In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level and thus determine the electrical conductivity of the solid. In electrical insulators and semiconductors, the valence band is the highest range of electron energies in which electrons are normally present at absolute zero temperature. For example, a silicon atom has fourteen electrons. In the ground state, they are arranged in the electron configuration [Ne]3s23p2. Of these, four are valence electrons, occupying the 3s orbital and two of the 3p orbitals. The distinction between the valence and conduction bands is meaningless in metals, because conduction occurs in one or more partially filled bands that take on the properties of both the valence and conduction bands.- Conduction Band. In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level and thus determine the electrical conductivity of the solid. In electrical insulators and semiconductors, the conduction band is the lowest range of vacant electronic states. On a graph of the electronic band structure of a material, the valence band is located below the Fermi level, while the conduction band is located above it. In semiconductors, electrons may reach the conduction band, when they are excited, for example, by ionizing radiation (i.e. they must obtain energy higher than Egap). For example, diamond is a wide-band gap semiconductor (Egap = 5.47 eV) with high potential as an electronic device material in many devices. On the other side, germanium has a small band gap energy (Egap = 0.67 eV), which requires to operate the detector at cryogenic temperatures. The distinction between the valence and conduction bands is meaningless in metals, because conduction occurs in one or more partially filled bands that take on the properties of both the valence and conduction bands.
- Band Gap. In solid-state physics, the energy gap or the band gap is an energy range between valence band and conduction band where electron states are forbidden. In contrast to conductors, electrons in a semiconductor must obtain energy (e.g. from ionizing radiation) to cross the band gap and to reach the conduction band. Band gaps are naturally different for different materials. For example, diamond is a wide-band gap semiconductor (Egap = 5.47 eV) with high potential as an electronic device material in many devices. On the other side, germanium has a small band gap energy (Egap = 0.67 eV), which requires to operate the detector at cryogenic temperatures.
- Fermi Level. The term “Fermi level” comes from Fermi-Dirac statistics, which describes a distribution of particles over energy states in systems consisting of fermions (electrons) that obey the Pauli exclusion principle. Since they cannot exist in identical energy states, Fermi level is the term used to describe the top of the collection of electron energy levels at absolute zero temperature. The Fermi level is the surface of Fermi sea at absolute zero where no electrons will have enough energy to rise above the surface. In metals, the Fermi level lies in the hypothetical conduction band giving rise to free conduction electrons. In semiconductors the position of the Fermi level is within the band gap, approximately in the middle of the band gap.
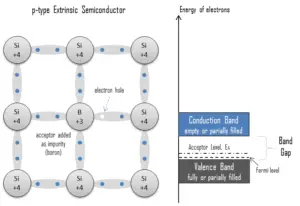 Electron-hole Pair. In the semiconductor, free charge carriers are electrons and electron holes(electron-hole pairs). Electrons and holes are created by excitation of electron from valence band to the conduction band. An electron hole (often simply called a hole) is the lack of an electron at a position where one could exist in an atom or atomic lattice. It is one of the two types of charge carriers that are responsible for creating electric current in semiconducting materials. Since in a normal atom or crystal lattice the negative charge of the electrons is balanced by the positive charge of the atomic nuclei, the absence of an electron leaves a net positive charge at the hole’s location. Positively charged holes can move from atom to atom in semiconducting materials as electrons leave their positions. When an electron meets with a hole, they recombine and these free carriers effectively vanish. The recombination means an electron which has been excited from the valence band to the conduction band falls back to the empty state in the valence band, known as the holes.
Electron-hole Pair. In the semiconductor, free charge carriers are electrons and electron holes(electron-hole pairs). Electrons and holes are created by excitation of electron from valence band to the conduction band. An electron hole (often simply called a hole) is the lack of an electron at a position where one could exist in an atom or atomic lattice. It is one of the two types of charge carriers that are responsible for creating electric current in semiconducting materials. Since in a normal atom or crystal lattice the negative charge of the electrons is balanced by the positive charge of the atomic nuclei, the absence of an electron leaves a net positive charge at the hole’s location. Positively charged holes can move from atom to atom in semiconducting materials as electrons leave their positions. When an electron meets with a hole, they recombine and these free carriers effectively vanish. The recombination means an electron which has been excited from the valence band to the conduction band falls back to the empty state in the valence band, known as the holes.
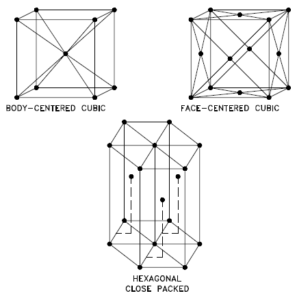
Uranium – Crystal Structure
A possible crystal structure of Uranium is orthorhombic structure.
In metals, and in many other solids, the atoms are arranged in regular arrays called crystals. A crystal lattice is a repeating pattern of mathematical points that extends throughout space. The forces of chemical bonding causes this repetition. It is this repeated pattern which control properties like strength, ductility, density, conductivity (property of conducting or transmitting heat, electricity, etc.), and shape. There are 14 general types of such patterns known as Bravais lattices.
The three most common basic crystal patterns are:
- Body-centered Cubic. In a body-centered cubic (BCC) arrangement of atoms, the unit cell consists of eight atoms at the corners of a cube and one atom at the body center of the cube. In a body-centered cubic arrangement, a unit cell contains (8 corner atoms × ⅛) + (1 center atom × 1) = 2 atoms. The packing is more efficient (68%) than simple cubic and the structure is a common one for alkali metals and early transition metals. Metals containing BCC structures include ferrite, chromium, vanadium, molybdenum, and tungsten. These metals possess high strength and low ductility.
- Face-centered Cubic.In a face-centered cubic (FCC) arrangement of atoms, the unit cell consists of eight atoms at the corners of a cube and one atom at the center of each of the faces of the cube. In a face-centered cubic arrangement, a unit cell contains (8 corner atoms × ⅛) + (6 face atoms × ½) = 4 atoms. This structure, along with its hexagonal relative (hcp), has the most efficient packing (74%). Metals containing FCC structures include austenite, aluminum, copper, lead, silver, gold, nickel, platinum, and thorium. These metals possess low strength and high ductility.
- Hexagonal Close-packed. In a hexagonal close-packed (HCP) arrangement of atoms, the unit cell consists of three layers of atoms. The top and bottom layers contain six atoms at the corners of a hexagon and one atom at the center of each hexagon. The middle layer contains three atoms nestled between the atoms of the top and bottom layers, hence, the name close-packed. Hexagonal close packed (hcp) is one of the two simple types of atomic packing with the highest density, the other being the face centered cubic (fcc). However, unlike the fcc, it is not a Bravais lattice as there are two nonequivalent sets of lattice points. Metals containing HCP structures include beryllium, magnesium, zinc, cadmium, cobalt, thallium, and zirconium. HCP metals are not as ductile as FCC metals.
–