Hydrogen
0.0899 g/cm3
Helium
0.1789 g/cm3
Lithium
0.535 g/cm3
Beryllium
1.848 g/cm3
Boron
2.46 g/cm3
Carbon
2.26 g/cm3
Nitrogen
1.251 g/cm3
Oxygen
1.429 g/cm3
Fluorine
1.696 g/cm3
Neon
0.9 g/cm3
Sodium
0.968 g/cm3
Magnesium
1.738 g/cm3
Aluminium
2.7 g/cm3
Silicon
2.33 g/cm3
Phosphorus
1.823 g/cm3
Sulfur
1.96 g/cm3
Chlorine
3.214 g/cm3
Argon
1.784 g/cm3
Potassium
0.856 g/cm3
Calcium
1.55 g/cm3
Scandium
2.985 g/cm3
Titanium
4.507 g/cm3
Vanadium
6.11 g/cm3
Chromium
7.14 g/cm3
Manganese
7.47 g/cm3
Iron
7.874 g/cm3
Cobalt
8.9 g/cm3
Nickel
8.908 g/cm3
Copper
8.92 g/cm3
Zinc
7.14 g/cm3
Gallium
5.904 g/cm3
Germanium
5.323 g/cm3
Arsenic
5.727 g/cm3
Selenium
4.819 g/cm3
Bromine
3.12 g/cm3
Krypton
3.75 g/cm3
Rubidium
1.532 g/cm3
Strontium
2.63 g/cm3
Yttrium
4.472 g/cm3
Zirconium
6.511 g/cm3
Niobium
8.57 g/cm3
Molybdenum
10.28 g/cm3
Technetium
11.5 g/cm3
Ruthenium
12.37 g/cm3
Rhodium
12.45 g/cm3
Palladium
12.023 g/cm3
Silver
10.49 g/cm3
Cadmium
8.65 g/cm3
Indium
7.31 g/cm3
Tin
7.31 g/cm3
Antimony
6.697 g/cm3
Tellurium
6.24 g/cm3
Iodine
4.94 g/cm3
Xenon
5.9 g/cm3
Caesium
1.879 g/cm3
Lanthanoids
Hafnium
13.31 g/cm3
Tantalum
16.65 g/cm3
Tungsten
19.25 g/cm3
Rhenium
21.02 g/cm3
Osmium
22.61 g/cm3
Iridium
22.65 g/cm3
Platinum
21.09 g/cm3
Gold
19.3 g/cm3
Mercury
13.534 g/cm3
Thallium
11.85 g/cm3
Lead
11.34 g/cm3
Bismuth
9.78 g/cm3
Polonium
9.196 g/cm3
Astatine
6.4 g/cm3
Radon
9.73 g/cm3
Francium
Radium
5.5 g/cm3
Actinoids
Rutherfordium
23.2 g/cm3
Dubnium
29.3 g/cm3
Seaborgium
35 g/cm3
Bohrium
37 g/cm3
Hassium
41 g/cm3
Meitnerium
37.4 g/cm3
Darmstadtium
34.8 g/cm3
Roentgenium
28.7 g/cm3
Copernicium
23.7 g/cm3
Nihonium
16 g/cm3
Flerovium
14 g/cm3
Moscovium
13.5 g/cm3
Livermorium
12.9 g/cm3
Tennessine
7.2 g/cm3
Oganesson
Lanthanum
6.146 g/cm3
Cerium
6.689 g/cm3
Praseodymium
6.64 g/cm3
Neodymium
7.01 g/cm3
Promethium
7.264 g/cm3
Samarium
7.353 g/cm3
Europium
5.244 g/cm3
Gadolinium
7.901 g/cm3
Terbium
8.219 g/cm3
Dysprosium
8.551 g/cm3
Holmium
8.795 g/cm3
Erbium
9.066 g/cm3
Thulium
9.321 g/cm3
Ytterbium
6.57 g/cm3
Lutetium
9.841 g/cm3
Actinium
10.07 g/cm3
Thorium
11.724 g/cm3
Protactinium
15.37 g/cm3
Uranium
19.05 g/cm3
Neptunium
20.45 g/cm3
Plutonium
19.816 g/cm3
Americium
13.78 g/cm3
Curium
13.51 g/cm3
Berkelium
14.78 g/cm3
Californium
15.1 g/cm3
Einsteinium
8.84 g/cm3
Fermium
Mendelevium
10.3 g/cm3
Nobelium
9.9 g/cm3
Lawrencium
16 g/cm3
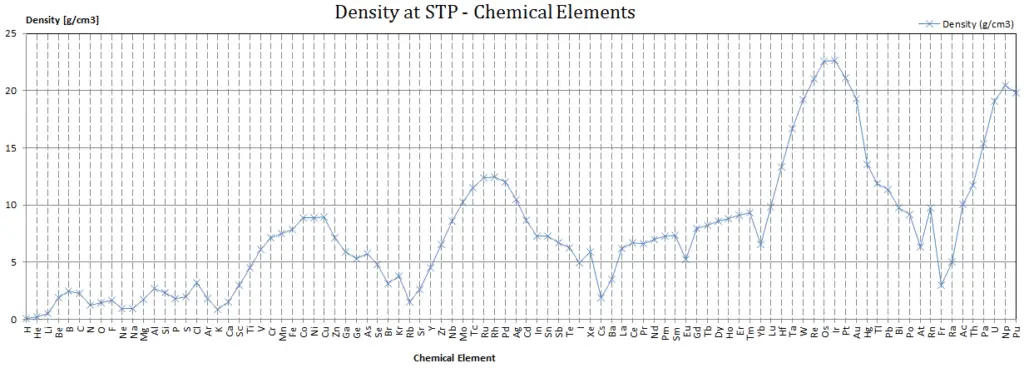
Density of Nobelium
Density of Nobelium is 9.9g/cm3.
Typical densities of various substances are at atmospheric pressure.
Density is defined as the mass per unit volume. It is an intensive property, which is mathematically defined as mass divided by volume:
ρ = m/V
In words, the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance. The standard SI unit is kilograms per cubic meter (kg/m3). The Standard English unit is pounds mass per cubic foot (lbm/ft3).
Density – Atomic Mass and Atomic Number Density
Since the density (ρ) of a substance is the total mass (m) of that substance divided by the total volume (V) occupied by that substance, it is obvious, the density of a substance strongly depends on its atomic mass and also on the atomic number density (N; atoms/cm3),
- Atomic Weight. The atomic mass is carried by the atomic nucleus, which occupies only about 10-12 of the total volume of the atom or less, but it contains all the positive charge and at least 99.95% of the total mass of the atom. Therefore it is determined by the mass number (number of protons and neutrons).
- Atomic Number Density. The atomic number density (N; atoms/cm3), which is associated with atomic radii, is the number of atoms of a given type per unit volume (V; cm3) of the material. The atomic number density (N; atoms/cm3) of a pure material having atomic or molecular weight (M; grams/mol) and the material density (⍴; gram/cm3) is easily computed from the following equation using Avogadro’s number (NA = 6.022×1023 atoms or molecules per mole):
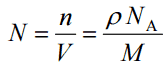
Since nucleons (protons and neutrons) make up most of the mass of ordinary atoms, the density of normal matter tends to be limited by how closely we can pack these nucleons and depends on the internal atomic structure of a substance. The densest material found on earth is the metal osmium, but its density pales by comparison to the densities of exotic astronomical objects such as white dwarf stars and neutron stars.
If we include man made elements, the densest so far is Hassium. Hassium is a chemical element with symbol Hs and atomic number 108. It is a synthetic element (first synthesised at Hasse in Germany) and radioactive. The most stable known isotope, 269Hs, has a half-life of approximately 9.7 seconds. It has an estimated density of 40.7 x 103 kg/m3. The density of Hassium results from its high atomic weight and from the significant decrease in ionic radii of the elements in the lanthanide series, known as lanthanide and actinide contraction.
Density – Pressure and Temperature
The density of a material varies with temperature and pressure. This variation is typically small for solids and liquids but much greater for gases. Most materials expand when their temperatures increase. Rising temperatures make the liquid expand in a liquid-in-tube thermometer and bend bimetallic strips. As a result of this expansion, the density of most materials decreases. This effect is caused by a decrease in the atomic number density. This dependence is usually expressed by the coefficient of linear or volume expansion.
Increasing the pressure on an material (especially for liquids or gases) decreases the volume of the object and thus increases its density via the atomic number density. Compressibility (also known as the coefficient of compressibility is a measure of the relative volume change of a fluid or solid as a response to a pressure (or mean stress) change.
See also: What is Density
See also: Densest Materials of the Earth
Atomic Mass of Nobelium
Atomic mass of Nobelium is 259 u.
The atomic mass is the mass of an atom. The atomic mass or relative isotopic mass refers to the mass of a single particle, and therefore is tied to a certain specific isotope of an element. The atomic mass is carried by the atomic nucleus, which occupies only about 10-12 of the total volume of the atom or less, but it contains all the positive charge and at least 99.95% of the total mass of the atom. Note that, each element may contain more isotopes, therefore this resulting atomic mass is calculated from naturally-occuring isotopes and their abundance.
The size and mass of atoms are so small that the use of normal measuring units, while possible, is often inconvenient. Units of measure have been defined for mass and energy on the atomic scale to make measurements more convenient to express. The unit of measure for mass is the atomic mass unit (amu). One atomic mass unit is equal to 1.66 x 10-24 grams. One unified atomic mass unit is approximately the mass of one nucleon (either a single proton or neutron) and is numerically equivalent to 1 g/mol.
For 12C the atomic mass is exactly 12u, since the atomic mass unit is defined from it. For other isotopes, the isotopic mass usually differs and is usually within 0.1 u of the mass number. For example, 63Cu (29 protons and 34 neutrons) has a mass number of 63 and an isotopic mass in its nuclear ground state is 62.91367 u.
There are two reasons for the difference between mass number and isotopic mass, known as the mass defect:
- The neutron is slightly heavier than the proton. This increases the mass of nuclei with more neutrons than protons relative to the atomic mass unit scale based on 12C with equal numbers of protons and neutrons.
- The nuclear binding energy varies between nuclei. A nucleus with greater binding energy has a lower total energy, and therefore a lower mass according to Einstein’s mass-energy equivalence relation E = mc2. For 63Cu the atomic mass is less than 63 so this must be the dominant factor.
Note that, it was found the rest mass of an atomic nucleus is measurably smaller than the sum of the rest masses of its constituent protons, neutrons and electrons. Mass was no longer considered unchangeable in the closed system. The difference is a measure of the nuclear binding energy which holds the nucleus together. According to the Einstein relationship (E=mc2), this binding energy is proportional to this mass difference and it is known as the mass defect.
See also: Atomic Mass Number – Does it conserve in a nuclear reaction?
Atomic Radius of Nobelium
The atomic radius of Nobelium atom is –pm (covalent radius).
It must be noted, atoms lack a well-defined outer boundary. The atomic radius of a chemical element is a measure of the distance out to which the electron cloud extends from the nucleus. However, this assumes the atom to exhibit a spherical shape, which is only obeyed for atoms in vacuum or free space. Therefore, there are various non-equivalent definitions of atomic radius.
- Van der Waals radius. In principle, Vana der Waals radius is half the minimum distance between the nuclei of two atoms of the element that are not bound to the same molecule.
- Ionic radius. An ionic radius is one-half the distance between the nuclei of two ions in an ionic bond.
- Covalent radius. Covalent radius is the nominal radius of the atoms of an element when covalently bound to other atoms.
- Metallic radius. A metallic radius is one-half the distance between the nuclei of two adjacent atoms in a crystalline structure, when joined to other atoms by metallic bonds.
On the periodic table of the elements, atomic radius tends to increase when moving down columns, but decrease when moving across rows (left to right). Consequently, the smallest atom is helium with a radius of 32 pm, while one of the largest is caesium at 225 pm. The atomic radii decrease across the periodic table because as the atomic number increases, the number of protons increases across the period, but the extra electrons are only added to the same quantum shell. Therefore, the effective nuclear charge towards the outermost electrons increases, drawing the outermost electrons closer. As a result, the electron cloud contracts and the atomic radius decreases.
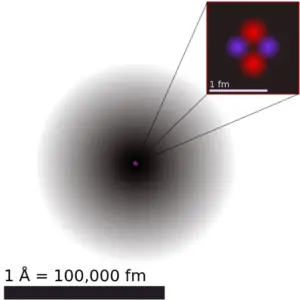
 The volume of an atom is about 15 orders of magnitude larger than the volume of a nucleus. For uranium atom, the Van der Waals radius is about 186 pm = 1.86 ×10−10m. The Van der Waals radius, rw, of an atom is the radius of an imaginary hard sphere representing the distance of closest approach for another atom. Assuming spherical shape, the uranium atom have volume of about 26.9 ×10−30 m3. But this “huge” space is occupied primarily by electrons, because the nucleus occupies only about 1721×10−45 m3 of space. These electrons together weigh only a fraction (let say 0.05%) of entire atom.
The volume of an atom is about 15 orders of magnitude larger than the volume of a nucleus. For uranium atom, the Van der Waals radius is about 186 pm = 1.86 ×10−10m. The Van der Waals radius, rw, of an atom is the radius of an imaginary hard sphere representing the distance of closest approach for another atom. Assuming spherical shape, the uranium atom have volume of about 26.9 ×10−30 m3. But this “huge” space is occupied primarily by electrons, because the nucleus occupies only about 1721×10−45 m3 of space. These electrons together weigh only a fraction (let say 0.05%) of entire atom.
It may seem, that the space and in fact the matter is empty, but it is not. Due to the quantum nature of electrons, the electrons are not point particles, they are smeared out over the whole atom. The classical description cannot be used to describe things on the atomic scale. On the atomic scale, physicists have found that quantum mechanics describes things very well on that scale. Particle locations in quantum mechanics are not at an exact position, they are described by a probability density function. Therefore the space in an atom (between electrons and an atomic nucleus) is not empty, but it is filled by a probability density function of electrons (usually known as “electron cloud“).
Nobelium – Crystal Structure
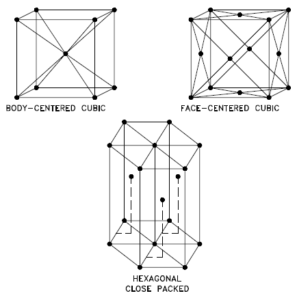
A possible crystal structure of Nobelium is face-centered cubic structure.
In metals, and in many other solids, the atoms are arranged in regular arrays called crystals. A crystal lattice is a repeating pattern of mathematical points that extends throughout space. The forces of chemical bonding causes this repetition. It is this repeated pattern which control properties like strength, ductility, density, conductivity (property of conducting or transmitting heat, electricity, etc.), and shape. There are 14 general types of such patterns known as Bravais lattices.
The three most common basic crystal patterns are:
- Body-centered Cubic. In a body-centered cubic (BCC) arrangement of atoms, the unit cell consists of eight atoms at the corners of a cube and one atom at the body center of the cube. In a body-centered cubic arrangement, a unit cell contains (8 corner atoms × ⅛) + (1 center atom × 1) = 2 atoms. The packing is more efficient (68%) than simple cubic and the structure is a common one for alkali metals and early transition metals. Metals containing BCC structures include ferrite, chromium, vanadium, molybdenum, and tungsten. These metals possess high strength and low ductility.
- Face-centered Cubic.In a face-centered cubic (FCC) arrangement of atoms, the unit cell consists of eight atoms at the corners of a cube and one atom at the center of each of the faces of the cube. In a face-centered cubic arrangement, a unit cell contains (8 corner atoms × ⅛) + (6 face atoms × ½) = 4 atoms. This structure, along with its hexagonal relative (hcp), has the most efficient packing (74%). Metals containing FCC structures include austenite, aluminum, copper, lead, silver, gold, nickel, platinum, and thorium. These metals possess low strength and high ductility.
- Hexagonal Close-packed. In a hexagonal close-packed (HCP) arrangement of atoms, the unit cell consists of three layers of atoms. The top and bottom layers contain six atoms at the corners of a hexagon and one atom at the center of each hexagon. The middle layer contains three atoms nestled between the atoms of the top and bottom layers, hence, the name close-packed. Hexagonal close packed (hcp) is one of the two simple types of atomic packing with the highest density, the other being the face centered cubic (fcc). However, unlike the fcc, it is not a Bravais lattice as there are two nonequivalent sets of lattice points. Metals containing HCP structures include beryllium, magnesium, zinc, cadmium, cobalt, thallium, and zirconium. HCP metals are not as ductile as FCC metals.
–